Karmaşık sayılar

faruk41 20:23 30 Eyl 2012 #1

Öncelikle merhaba , 5 tane sorum olacak. Şimdiden yardım eden arkadaşlara,hocalarımıza teşekkürler.

1)z1=1+3i , z2=3+i , z3=3+4i , z4=4+3i karmaşık sayılarının karmaşık düzlemde köşelerini oluşturduğu dörtgenin alanı kaç br² dir?
CEVAP: 9/2 br²

2) z=x+i / 2+i karmaşık sayısı için Re(z)+Im(z)=2 olduğuna göre , x kaçtır?
CEVAP: 7

3) z=a/b - ib/3 olmak üzere |z'nin eşleniği/-z| ifadesinin eşiti kaçtır?
CEVAP:1

4) z1=3+i , z2=1-3i , z3=√5 + 2i olduğuna göre |z1.z3 / z2| işleminin sonucu kaçtır?
CEVAP:3

5)i üzeri 7 + i üzeri 8 + i üzeri 9 .... + i üzeri 77 işleminin sonucu aşağıdakilerden hangisidir?
CEVAP:1

ezekiel 06:25 01 Eki 2012 #2

Cevap 5
i⁷=-i
i⁸=1
i⁹=i
i¹⁰=-1
Bu şekilde 71 tane terim var ve sırayla 4 terimin toplamı sıfır oluyor dikkat edersen 71/4 bölümünden kalan 3 tür.
Sırasıyla -i,1 ve i terimleri kalır bunların toplamları da 1 olur.
Not=
i⁷=i³=-i
i⁸=i^o=1 olur burda üssü 4 e böl ve kalanı üs olarak kullan
i⁴=1 olduğu için bunu yapıyoruz

ezekiel 07:31 01 Eki 2012 #3

Cevap 2

payı ve paydayı 2-i ile yani eşlenikle çarp

z=(x+i).(2-i)/5=(2x+1)/5+(2-x)i/5

(2x+1+2-x)/5=2

x+3=10 x=7 olur.

ezekiel 11:44 01 Eki 2012 #4

Cevap 4
Bu soruda karmaşık sayıların tek tek mutlak değerlerini alabilirsin.
|z1|=√10
|z2|=√10
|z3|=√9=3
|z1|.|z3|/|z2|=3 olur.

faruk41 19:29 01 Eki 2012 #5

Çok teşekkürler. Diğer sorularada bakabilir misiniz.

CIA 00:01 02 Eki 2012 #6

soru 1 için soru karmaşık sayı sorusu gibi değil sanki dörtgen sorusu gibi arkadaşım verilen noktaları kordinat düzlemine yerleştirdiğinde dörtgenlerdeki 1/2labl.lcdl köşegenlerden alan bulma formulunu uygularsan cevap 9/2 çıkıcaktır.

ezekiel 01:52 02 Eki 2012 #7

faruk41'den alıntı

Çok teşekkürler. Diğer sorularada bakabilir misiniz.

Yardımım olduysa ne mutlu bana

Cevap 3

z=a/b-bi/3

z=a/b+bi/3

-z=-a/b+bi/3

|z/-z|=|z|/|-z|

Dikkat edersen bu ifadede pay ve payda eşit olacak bölümleri de o yüzden 1 olur.

Not=Örnek (-a)²=(a)² Anlatmak istediğim (-) olmasının bir önemi kalmıyor.

ezekiel 02:46 02 Eki 2012 #8

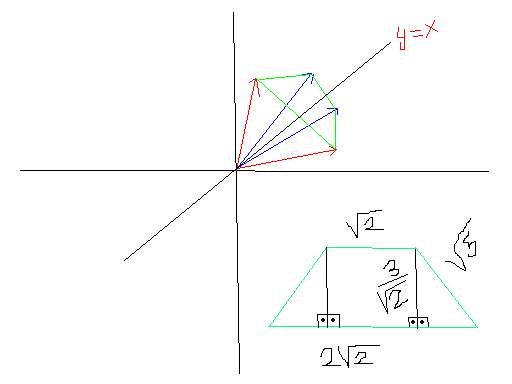
Şekle bakarsan iki karmaşık sayı y=x doğrusuna göre simetrik oluyor onları aynı renk çizdim.

Burada ikizkenar bir yamuk oluşuyor.

Karmaşık sayılar arasındaki uzaklıktan yamuğun kenarlarını buluyoruz.

Tüm kenarları bulduktan sonra yüksekliği bulduk.

Yamuğun alanı=(alt taban+üst taban).(yükseklik)/2 olur.

İşlemleri yaparsan 9/2 bulursun sonucu.

Belki alternatif kolay bir çözüm vardır.