1) II.bölgede eksenlere teğet ve yarıçapı 3birim olan çemberin denklemini bulunuz?
2)Koordinat düzleminde x=-4,y=4 ve eksenler arasında kalan dörtgenin iç teğet çemberinin denklemini bulunuz.
3)Merkezi x ekseni üzerinde bulunan ve x=-1 ile x=7 doğrularına teğet olan çemberin denklemini bulunuz
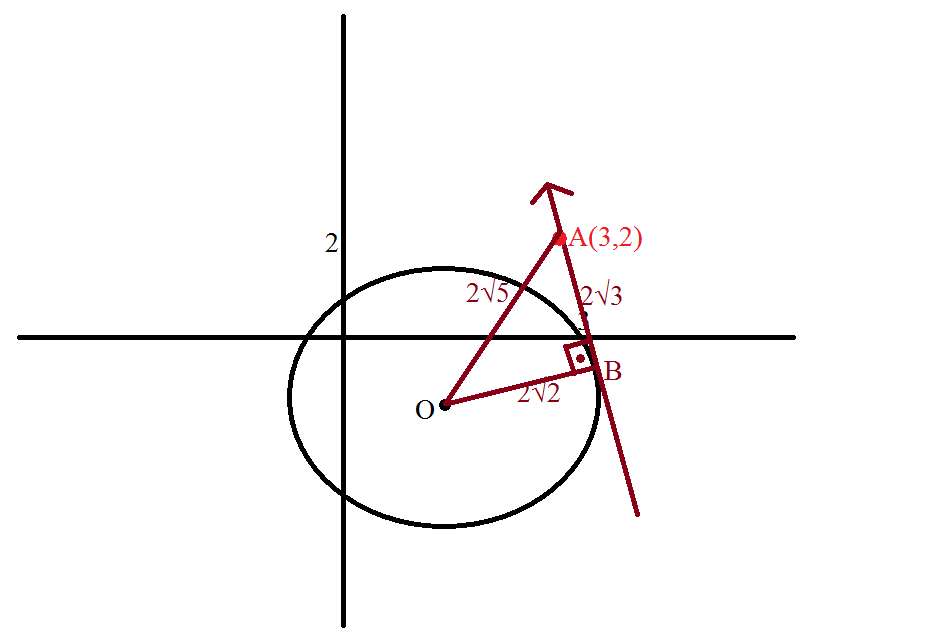
4)(x-1)²+(y+2)²=8 çemberine K(3,2) noktasından çizilen teğetin uzunluğu kaç birimdir.
5)x-y-1=0 doğrusu ile (x+1)²+(y-2)²=9 çemberinin kesişti noktaları arasındaki uzaklık kaç birimdir?
şimdiden çok teşekkür ederim.