1) II.bölgede eksenlere teğet ve yarıçapı 3birim olan çemberin denklemini bulunuz?
2)Koordinat düzleminde x=-4,y=4 ve eksenler arasında kalan dörtgenin iç teğet çemberinin denklemini bulunuz.
3)Merkezi x ekseni üzerinde bulunan ve x=-1 ile x=7 doğrularına teğet olan çemberin denklemini bulunuz
4)(x-1)²+(y+2)²=8 çemberine K(3,2) noktasından çizilen teğetin uzunluğu kaç birimdir.
5)x-y-1=0 doğrusu ile (x+1)²+(y-2)²=9 çemberinin kesişti noktaları arasındaki uzaklık kaç birimdir?
şimdiden çok teşekkür ederim.
2)Koordinat düzleminde x=-4,y=4 ve eksenler arasında kalan dörtgenin iç teğet çemberinin denklemini bulunuz.
3)Merkezi x ekseni üzerinde bulunan ve x=-1 ile x=7 doğrularına teğet olan çemberin denklemini bulunuz
4)(x-1)²+(y+2)²=8 çemberine K(3,2) noktasından çizilen teğetin uzunluğu kaç birimdir.
5)x-y-1=0 doğrusu ile (x+1)²+(y-2)²=9 çemberinin kesişti noktaları arasındaki uzaklık kaç birimdir?
şimdiden çok teşekkür ederim.
Diğer soruları yapamam ama 1. soruya kendi ürettiğim bir metodum var.
Çemberin denklemini bulmak için çemberin merkezini orijin yapmamız gerekiyor. Yani noktaların asıl orijine göre verilen koordinatlarını çemberin merkezine göre koordinata çevirip; daha sonra x'i ile y'sinin karelerinin toplamını çemberin yarıçapının karesine eşitlememiz gerekiyor.(Bu kareleri toplamı mevzusu; çemberin merkezinin çember üzerindeki bir noktaya olan uzaklığını pisagorla bulmamız için. Çünkü zaten bu uzaklık çemberin üzerindeki hiçbir noktada değişmez ve yarıçapa eşittir. )
Bu çemberin merkezi olan (-3,3) noktasını orijin yapmak için x'ine 3 ekleyip y'sinden 3 çıkarmamız gerekiyor. Çemberin yarıçapı da 3 olduğuna göre denklemi şöyle olur:
(x+3)²+(y-3)²=9
Çemberin denklemini bulmak için çemberin merkezini orijin yapmamız gerekiyor. Yani noktaların asıl orijine göre verilen koordinatlarını çemberin merkezine göre koordinata çevirip; daha sonra x'i ile y'sinin karelerinin toplamını çemberin yarıçapının karesine eşitlememiz gerekiyor.(Bu kareleri toplamı mevzusu; çemberin merkezinin çember üzerindeki bir noktaya olan uzaklığını pisagorla bulmamız için. Çünkü zaten bu uzaklık çemberin üzerindeki hiçbir noktada değişmez ve yarıçapa eşittir. )
Bu çemberin merkezi olan (-3,3) noktasını orijin yapmak için x'ine 3 ekleyip y'sinden 3 çıkarmamız gerekiyor. Çemberin yarıçapı da 3 olduğuna göre denklemi şöyle olur:
(x+3)²+(y-3)²=9
Diğer soruları yapamam, dedim ama önyargılı olmamak gerekiyormuş. 2 de çıktı.
Bu dörtgeni çizersek; bir kenari 4 br. olan bir kare olur. Karenin iç teğet çemberinin merkezi de köşegenlerin kesim noktası olduğuna göre bu çemberin merkezi (-2,2) noktası. Çapı da mutlaka karenin bir kenarına eşit yani 4 olduğuna göre yarıçapı 2 br. olmalı.
Yine 1. soruyla aynı mantıktan çemberin denklemi;
(x+2)²+(y-2)²=4 olur.
Bu dörtgeni çizersek; bir kenari 4 br. olan bir kare olur. Karenin iç teğet çemberinin merkezi de köşegenlerin kesim noktası olduğuna göre bu çemberin merkezi (-2,2) noktası. Çapı da mutlaka karenin bir kenarına eşit yani 4 olduğuna göre yarıçapı 2 br. olmalı.
Yine 1. soruyla aynı mantıktan çemberin denklemi;
(x+2)²+(y-2)²=4 olur.
3 de çıktı.
Bı çemberi çizersek çapını 8 buluruz. Yarı çapı da 4 olur. Şimdi merkezi de x ekseninde olduğuna göre (3,0) noktasında olmalı. İki teğete de eşit mesafede olması için. Yine aynı mantıktan denklemi şöyle olur:
(x-3)²+y²=16
Bı çemberi çizersek çapını 8 buluruz. Yarı çapı da 4 olur. Şimdi merkezi de x ekseninde olduğuna göre (3,0) noktasında olmalı. İki teğete de eşit mesafede olması için. Yine aynı mantıktan denklemi şöyle olur:
(x-3)²+y²=16
Benimki biraz elipse benzedi ama idare edersin artık. 

Çözümü şöyle:
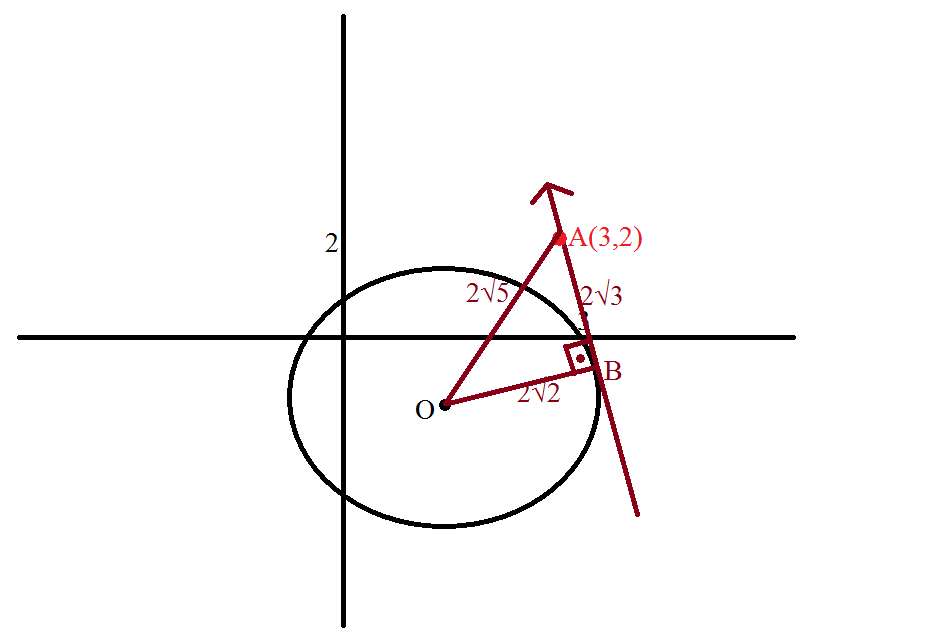
O ile A arasındaki uzaklığı iki nokta arası uzaklık formülünden bulduk.
Yarıçapı; denklemden dolayı √8=2√2 bulduk.
Merkezle teğeti birleştirirsek teğete dik olur, dedik ve pisagordan cevabı 2√3 bulduk.
Çözümü şöyle:
O ile A arasındaki uzaklığı iki nokta arası uzaklık formülünden bulduk.
Yarıçapı; denklemden dolayı √8=2√2 bulduk.
Merkezle teğeti birleştirirsek teğete dik olur, dedik ve pisagordan cevabı 2√3 bulduk.
Mat. sen 9. sınıf olduğuna emin misin 
Mat. sen 9. sınıf olduğuna emin misin 
Son soruyu da çözüyorum bu arada.
Evet,eminim, 9. sınıfım ama meraklıyım matematiğe, geometriye. 
Son soruyu da çözüyorum bu arada.
Son soruyu da çözüyorum bu arada.

