mervsenlik 14:46 26 Şub 2011 #1
S-1)
S_2)
S-3) Bir ABC üçgeninde b²=a²+c²-√3.a.c ise B açısının ölçüsü kaç derecedir?
S-5) sinC=cosA+cosB ise ABC üçgeninin dik üçgen olduğunu gösteriniz.
S_2)
S-3) Bir ABC üçgeninde b²=a²+c²-√3.a.c ise B açısının ölçüsü kaç derecedir?
S-4)
sinA
sinB
=2.cosC ise ABC üçgeninin ikizkenar üçgen olduğunu gösteriniz.
S-5) sinC=cosA+cosB ise ABC üçgeninin dik üçgen olduğunu gösteriniz.
gereksizyorumcu 15:37 26 Şub 2011 #2
C-1)
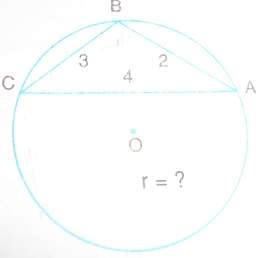
A(ABC)=a.b.c/4R → R=abc/4A
Herondan alanı yazarsak (4 katını yazalım kolaylık olsun)
4A=√9.5.3.1=3√15
→ R=2.3.4/3√15=8/√15=8√15/15
C-2)
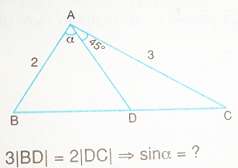
AD açıortaydır , a=45º bulunur
sinüs teoremini muhakkak kullanalım diyorsan
iki küçük üçgende sinüs teoremi yazılır D köşesindeki açının sinüsleri birbirini 180 e tamamladığından eşit olur oradan sina=sin45 bulunur , a=45 veya 135 olur ama a=135 için üçgen olmaz. cevap 45tir
C-3)
bu direkt cosinüs teoreminin yazımı
cosb=√3/2 yani B açısı 30º dir.
inan şekilleri scroll yapıp tekrar bakmak soruları çözüp yazmaktan daha zor, bundan sonra bu kadar büyük resimler yüklemezsen daha güzel olur, sorunun anlaşılabilecei mümkün olan en düşük çözünürlükte eklemen yeterli sanırım
A(ABC)=a.b.c/4R → R=abc/4A
Herondan alanı yazarsak (4 katını yazalım kolaylık olsun)
4A=√9.5.3.1=3√15
→ R=2.3.4/3√15=8/√15=8√15/15
C-2)
AD açıortaydır , a=45º bulunur
sinüs teoremini muhakkak kullanalım diyorsan
iki küçük üçgende sinüs teoremi yazılır D köşesindeki açının sinüsleri birbirini 180 e tamamladığından eşit olur oradan sina=sin45 bulunur , a=45 veya 135 olur ama a=135 için üçgen olmaz. cevap 45tir
C-3)
bu direkt cosinüs teoreminin yazımı
cosb=√3/2 yani B açısı 30º dir.
inan şekilleri scroll yapıp tekrar bakmak soruları çözüp yazmaktan daha zor, bundan sonra bu kadar büyük resimler yüklemezsen daha güzel olur, sorunun anlaşılabilecei mümkün olan en düşük çözünürlükte eklemen yeterli sanırım
Şekil haricindeki soruları konu açarken kullandığnız editördeki sembolleri ile yazabilirsiniz. Bir çok matematik sembolü vardır.
gereksizyorumcu 15:48 26 Şub 2011 #4
C-4)
sinA/sinB=a/b olduğunu sinüs teoreminden biliyoruz
c için cosinüs teoremini yazalım
c²=a²+b²-2.cosC.a.b , burada 2cosC yerine a/b yazıldığında
c²=a²+b²-a²b/b=b² bulunur yani c²=b² dir
bunlar pozitif uzunluklar olduğundan b=c bulunur üçgen ikizkenardır
sinA/sinB=a/b olduğunu sinüs teoreminden biliyoruz
c için cosinüs teoremini yazalım
c²=a²+b²-2.cosC.a.b , burada 2cosC yerine a/b yazıldığında
c²=a²+b²-a²b/b=b² bulunur yani c²=b² dir
bunlar pozitif uzunluklar olduğundan b=c bulunur üçgen ikizkenardır
gereksizyorumcu 16:28 26 Şub 2011 #5
C-5)
C=180-A-B olduğundan
sinC=sin(A+B) dir
cosA+cosB ye dönüşüm uygularsak = 2.cos((A+B)/2).cos((A-B)/2) elde ederiz
sin(A+B) yi de 2.sin((A+B)/2).cos((A+B)/2) şeklinde yazdğımızda +lı cosinüsler sadeleşir
cos((A-B)/2)=sin((A+B)/2) kalır
burada bir açının sinüsü diğerinin cosinüsüne eşitse toplamları 90 dır.
(A-B)/2+(A+B)/2=90 → A=90 bulunur. bu bir diküçgendir.
C=180-A-B olduğundan
sinC=sin(A+B) dir
cosA+cosB ye dönüşüm uygularsak = 2.cos((A+B)/2).cos((A-B)/2) elde ederiz
sin(A+B) yi de 2.sin((A+B)/2).cos((A+B)/2) şeklinde yazdğımızda +lı cosinüsler sadeleşir
cos((A-B)/2)=sin((A+B)/2) kalır
burada bir açının sinüsü diğerinin cosinüsüne eşitse toplamları 90 dır.
(A-B)/2+(A+B)/2=90 → A=90 bulunur. bu bir diküçgendir.
Diğer çözümlü sorular alttadır.
Kosinüs Teoremi Soruları Çözümleri Sinüs Teoremi Soruları Çözümleri Trigonometri Soruları Trigonometri Soruları ve Çözümleri Trigonometri Üçgen Soruları Çözümleri
Tüm Etiketler
Tüm Etiketler