SORU1 
SORU2
SORU3 P(x) polinomunun (x+2) ile bölümünden kalan 7, (x-1) ile bölümünden kalan 1 ise bu polinomun (x²+x-2) ile bölümünden kalan nedir?
SORU4 P(x) = x³+ax²+bx polinomu (x²+1) ile bölündüğünde (2x-4) kalanını verdiğine göre a.b kaçtır?
SORU5 Üçüncü dereceden bir P(x) polinomu(x+2),(x+3) ve (x-4) ile tam bölünüyor. P(5)= -56 ise P(3) kaçtır?
NOT:Fotoğraflarda okunmayan kısımlar:
Soru 1'de sırayla üslü ifadeler : p³ , x² , x²
Soru 2'de sırayla üslü ifadeler : x³ , x² (Birinci payda x³, en sağdaki payda x²)
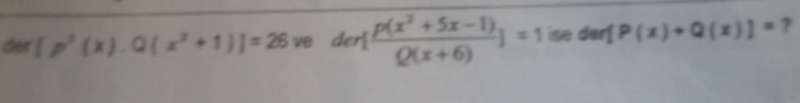
SORU2
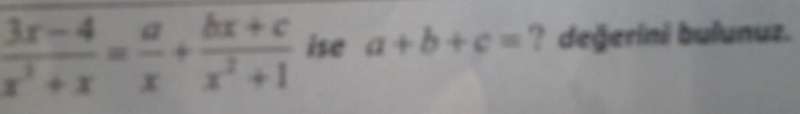
SORU3 P(x) polinomunun (x+2) ile bölümünden kalan 7, (x-1) ile bölümünden kalan 1 ise bu polinomun (x²+x-2) ile bölümünden kalan nedir?
SORU4 P(x) = x³+ax²+bx polinomu (x²+1) ile bölündüğünde (2x-4) kalanını verdiğine göre a.b kaçtır?
SORU5 Üçüncü dereceden bir P(x) polinomu(x+2),(x+3) ve (x-4) ile tam bölünüyor. P(5)= -56 ise P(3) kaçtır?
NOT:Fotoğraflarda okunmayan kısımlar:
Soru 1'de sırayla üslü ifadeler : p³ , x² , x²
Soru 2'de sırayla üslü ifadeler : x³ , x² (Birinci payda x³, en sağdaki payda x²)
5.soru
p(x) polinomu (x+2),(x+3),(x-4) ile tam bölünüyorsa
P(x)=a.(x-4).(x+2).(x+3) şeklinde yazılabilir. p(x) 3. dereceden olduğu için ve bu üç bölenin çarpımları 3. dereceden bir denklem oluşturduğu için böyle yazılır.a ise bize başkatsayısını vermediği için yazılır. x=5 için -56 vermeli.
P(5)=-56=a.1.7.8
a=-1 gelir. yani p(x) polinomu -(x-4)(x+2)(x+3)=P(x) şeklindedir.
p(3)=-(-7)(5)(6)=210 gelmeli.
p(x) polinomu (x+2),(x+3),(x-4) ile tam bölünüyorsa
P(x)=a.(x-4).(x+2).(x+3) şeklinde yazılabilir. p(x) 3. dereceden olduğu için ve bu üç bölenin çarpımları 3. dereceden bir denklem oluşturduğu için böyle yazılır.a ise bize başkatsayısını vermediği için yazılır. x=5 için -56 vermeli.
P(5)=-56=a.1.7.8
a=-1 gelir. yani p(x) polinomu -(x-4)(x+2)(x+3)=P(x) şeklindedir.
p(3)=-(-7)(5)(6)=210 gelmeli.
4.soru
x2+1'e bölümünden kalan 2x-4 ve bölüm Q(x) olsun.
P(x)=(x2+1).Q(x)+(2x-4) şeklinde yazılır. x2=-1 yazdığında bölen sıfırlanır ve geriye kalan kalır. polinomda x2 gördüğün yere -1 yaz. çıkan sonuç kalana eşit olmalı.
x.(-1)+a(-1)+bx=2x-4
(b-1)x-a=2x-4
a=4
b=2 gelir. çarpımları da 8
x2+1'e bölümünden kalan 2x-4 ve bölüm Q(x) olsun.
P(x)=(x2+1).Q(x)+(2x-4) şeklinde yazılır. x2=-1 yazdığında bölen sıfırlanır ve geriye kalan kalır. polinomda x2 gördüğün yere -1 yaz. çıkan sonuç kalana eşit olmalı.
x.(-1)+a(-1)+bx=2x-4
(b-1)x-a=2x-4
a=4
b=2 gelir. çarpımları da 8
3.soru
p(x)=(x+2).m+7 şeklinde yaz. burada m bölüm.
P(x)=(x-1).n+1 burada n bölüm.
x2+x-2=(x-1)(x+2) şeklinde yazılır.
P(x)'in (x-1).(x+2) ile bölümünden kalan ax+b olsun.
p(x)=(x-1)(x+2).c+(ax+b) şeklinde yazılır.
x=1 ve x=-2 için iki farklı denklem bulacaksın ve oradan a ile b'yi bul.
p(x)=(x+2).m+7 şeklinde yaz. burada m bölüm.
P(x)=(x-1).n+1 burada n bölüm.
x2+x-2=(x-1)(x+2) şeklinde yazılır.
P(x)'in (x-1).(x+2) ile bölümünden kalan ax+b olsun.
p(x)=(x-1)(x+2).c+(ax+b) şeklinde yazılır.
x=1 ve x=-2 için iki farklı denklem bulacaksın ve oradan a ile b'yi bul.
2.soru
sağ tarafta payda eşitleyin. paydalar aynı oluyor. o halde paylarda aynı olmalı. oradan a,b,c değerlerini bulursunuz.
sağ tarafta payda eşitleyin. paydalar aynı oluyor. o halde paylarda aynı olmalı. oradan a,b,c değerlerini bulursunuz.
1.soru
(bu sorunun çözümüne bakmadan önce derece ile ilgili özelliklere bakın)
derP(X)=m olsun.
derQ(x)=n olsun.
Q(x) polinomu x yerine x2 ifadesi katılmış. oradaki +1 önemsiz. (özelliklerde var)
derQ(x)=n ise derQ(x2)=2n olur.
derp(x)3=3m gelir.
derQ(x2).P(x)3=3m+2n=26 gelir.
aynı şeyi 2. verilende uygula.
derP(x2...)=2m gelir.
derQ(x+6)=n gelir.
2m-n=1 elinde birinci dereceden 2 bilinmeyenli denklem var. buradan n ve m'i bul
der(p(x)+Q(x)) ise hangisinin derecesi büyük ise o yazılırdı.
(bu sorunun çözümüne bakmadan önce derece ile ilgili özelliklere bakın)
derP(X)=m olsun.
derQ(x)=n olsun.
Q(x) polinomu x yerine x2 ifadesi katılmış. oradaki +1 önemsiz. (özelliklerde var)
derQ(x)=n ise derQ(x2)=2n olur.
derp(x)3=3m gelir.
derQ(x2).P(x)3=3m+2n=26 gelir.
aynı şeyi 2. verilende uygula.
derP(x2...)=2m gelir.
derQ(x+6)=n gelir.
2m-n=1 elinde birinci dereceden 2 bilinmeyenli denklem var. buradan n ve m'i bul
der(p(x)+Q(x)) ise hangisinin derecesi büyük ise o yazılırdı.
2.soru
sağ tarafta payda eşitleyin. paydalar aynı oluyor. o halde paylarda aynı olmalı. oradan a,b,c değerlerini bulursunuz.
sağ tarafta payda eşitleyin. paydalar aynı oluyor. o halde paylarda aynı olmalı. oradan a,b,c değerlerini bulursunuz.
birde 1 ve3. soruları daha açık yazabilir misiniz cevaplarıyla birlikte.1.soruda UST ve SUT yazıyor :/
sağlık sorunum yüzünden okulun 4.haftasını kaçırdım polinomların bu konusuyla ilgili fazla birşey bilmiyorum.
2.soru
payda eşitleyin. a/x 'i x2 ise öteki ifadeyi ise x ile genişletin. kısaca sağ taraftakilerin paydalarını eşitleyip toplayın.
o ust ve sut üssü yazımını yanlış yazmışım. düzeltiyorum.
payda eşitleyin. a/x 'i x2 ise öteki ifadeyi ise x ile genişletin. kısaca sağ taraftakilerin paydalarını eşitleyip toplayın.
o ust ve sut üssü yazımını yanlış yazmışım. düzeltiyorum.
3.soru
tüm bölme işlemlerinin yazımı vardır. bölünen sayı=bölüm.bölen+kalan.
p(x)'in x+2 ile bölümünden kalan 7. bölüm m olsun.
p(x)=(x+2).m+7 şeklinde yazılır.
x=-2 için m.(x+2) sıfırlanır ve sonuç kalan olur.
P(-2)=7
aynı şey x-1 ile bölümü için de mümkün. x-1 ile bölümünden kalan 1. bölüm n olsun.
p(x)=(x-1).n+1 şeklinde yazılır. ve aynı şey bunun içinde geçerli. x=1 için bölüm ile bölenin çarpımları 0 olur ve elde kalan kalır.
P(1)=1
x2+x-2=(x-1)(x+2) şeklinde çarpanlarına ayrılır.
p(x)'in x[UST]2[/USY]+x-2 ile bölümünden kalan ax+b olsun. bölüm de c olsun. üsttekiler gibi yazın. fakat çarpanlarına ayrılmış şekilde.
P(x)=(x-1)(x+2).c+(ax+b) x=-2 için bölüm ile bölenlerin çarpımı sıfır olur ve elde kalan kalır.
x=-2 için
p(-2)=-2a+b=7
x=1 için
P(1)=a+b=1 birinci dereceden iki bilinmeyenli denklem oluştu. bunları taraf tarafa çıkar.
-3a=6
a=-2
b=3 gelir. yani P(x)'in x2+x-2 ile bölümünden kalan ax+b=-2x+3
forumdan matematik arşivinden varsa polinomlarda dereceye bakın veya elinizdeki kaynaktan. 1. sorudaki çözüm sadece derecelerdeki özellikleri kullanarak yaptım. anlamazsanız mesaj atın. açıklayarak yazayım.
tüm bölme işlemlerinin yazımı vardır. bölünen sayı=bölüm.bölen+kalan.
p(x)'in x+2 ile bölümünden kalan 7. bölüm m olsun.
p(x)=(x+2).m+7 şeklinde yazılır.
x=-2 için m.(x+2) sıfırlanır ve sonuç kalan olur.
P(-2)=7
aynı şey x-1 ile bölümü için de mümkün. x-1 ile bölümünden kalan 1. bölüm n olsun.
p(x)=(x-1).n+1 şeklinde yazılır. ve aynı şey bunun içinde geçerli. x=1 için bölüm ile bölenin çarpımları 0 olur ve elde kalan kalır.
P(1)=1
x2+x-2=(x-1)(x+2) şeklinde çarpanlarına ayrılır.
p(x)'in x[UST]2[/USY]+x-2 ile bölümünden kalan ax+b olsun. bölüm de c olsun. üsttekiler gibi yazın. fakat çarpanlarına ayrılmış şekilde.
P(x)=(x-1)(x+2).c+(ax+b) x=-2 için bölüm ile bölenlerin çarpımı sıfır olur ve elde kalan kalır.
x=-2 için
p(-2)=-2a+b=7
x=1 için
P(1)=a+b=1 birinci dereceden iki bilinmeyenli denklem oluştu. bunları taraf tarafa çıkar.
-3a=6
a=-2
b=3 gelir. yani P(x)'in x2+x-2 ile bölümünden kalan ax+b=-2x+3
forumdan matematik arşivinden varsa polinomlarda dereceye bakın veya elinizdeki kaynaktan. 1. sorudaki çözüm sadece derecelerdeki özellikleri kullanarak yaptım. anlamazsanız mesaj atın. açıklayarak yazayım.
2.soru
payda eşitleyin. a/x 'i x2 ise öteki ifadeyi ise x ile genişletin. kısaca sağ taraftakilerin paydalarını eşitleyip toplayın.
o ust ve sut üssü yazımını yanlış yazmışım. düzeltiyorum.
payda eşitleyin. a/x 'i x2 ise öteki ifadeyi ise x ile genişletin. kısaca sağ taraftakilerin paydalarını eşitleyip toplayın.
o ust ve sut üssü yazımını yanlış yazmışım. düzeltiyorum.
