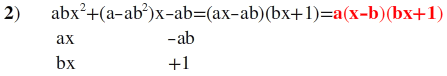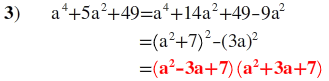1)
x=∛3-4 olduğuna göre
(x+5)³-3(x+5)²+3(x+5)+1 ifadesinin değeri kaçtır? (cevap 5)
-----------------------------
2) Aşağıdaki ifadelerden hangisi
abx²+(a-ab²)x-ab ifadesinin çarpanlarından biri değildir?
A) x-b B)bx+1 C)ax-ab D)a E)bx-a (cevap E)
-----------------------
3)
a⁴+5a²+49 ifadesinin çarpanlarından biri aşağıdakilerden hangisidir?
A)a²+5a+3 B)a²-3a+7 C)a²-3a-7 D)a²-5a+7 E)a²+7a+3 (cevap B)
---------------------------
4)
x³+3x²+3x+28 ifadesinin çarpanlarından biri aşağıdakilerden hangisidir?
A)x-3 B)x+1 C)x²+x+7 D)x²+x+4 E)x²-x+7 (cevap E)
------------------------
5)
x¹⁵-1=(x-1)(x⁴+x³+x²+x+1)(x10 + xk + 1) açılımına göre k kaçtır? (cevap 5)
--------------------