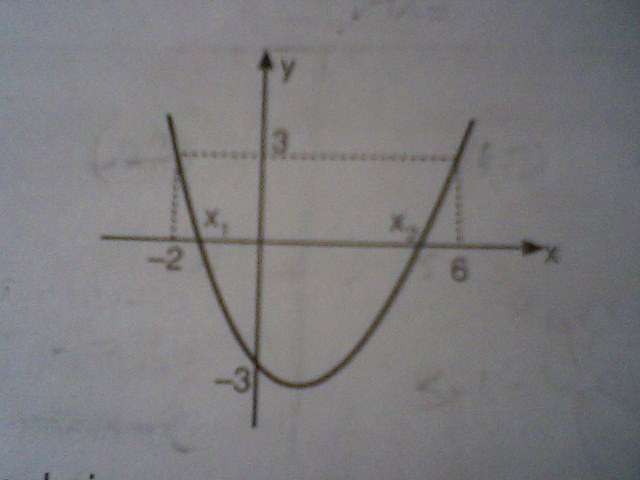
y=f(x) fonksiyonunun grafiği verilmiştir.
x₁+x₂ toplamı kaçtır?
A)1 B)2 C)3 D)4 E)5
Başında çok uğraştım. Çözen olursa çok sevinirim.
Parabol sağ tarafa ve sol tarafa göre simetrik olduğundan aynı y değerine giden x'ler toplamı sabittir.3'e giden x değerleri toplamı 4 olduğuna göre 0'a giden x değerleri toplamı da 4 olmalı.Ya da,
Parabolün denklemi y = ax^2 + bx + c şeklinde olacağına göre,
x = 0 için y = -3 oluyormuş, yani c = -3, denklemimiz ax^2 + bx - 3(gerçi buna gerek olmayacak)
x = -2 için y = 3müş
4a - 2b - 3 = 3
4a - 2b = 6
2a - b = 3
x = 6 için y = 3müş
36a - 6b - 3 = 3
36a - 6b = 6
6a - b = 1
İki denkleme ortak çözüm yaparsak a = 1/2, b = - 2 çıkar.Yani parabolün denklemi:
y = (x^2)/2 - 2x - 3 şeklindeymiş.
kökler toplamı -b/a'dan 2 / (1/2) = 4.
Parabolün denklemi y = ax^2 + bx + c şeklinde olacağına göre,
x = 0 için y = -3 oluyormuş, yani c = -3, denklemimiz ax^2 + bx - 3(gerçi buna gerek olmayacak)
x = -2 için y = 3müş
4a - 2b - 3 = 3
4a - 2b = 6
2a - b = 3
x = 6 için y = 3müş
36a - 6b - 3 = 3
36a - 6b = 6
6a - b = 1
İki denkleme ortak çözüm yaparsak a = 1/2, b = - 2 çıkar.Yani parabolün denklemi:
y = (x^2)/2 - 2x - 3 şeklindeymiş.
kökler toplamı -b/a'dan 2 / (1/2) = 4.
çok teşekkür ederim.
