1--)) 3 basamaklı abc doğal sayısı 15 ile tam bölünebilen bir tek sayıdır . a>b>c ise ,kaç farklı abc sayısı yazılabilir ?
2--)) A≥B olmak üzere , üç basamaklı A7B doğal sayısının 4 ile bölümünden kalan 1 dir .Bu sayı 3 ile bölünebildiğine göre ,A nın alacağı değerler toplamı kaçtır ??
3--)) -1 < x < (16 / x) eşitsizliğini sağlayan x değerlerinin bulunduğu en geniş aralık nedir ?
4--)) f: [3,5] → R f(x)= x² - 4x fonksiyonunun alacağı en büyük değer ,en küçük değerden kaç fazladır ?
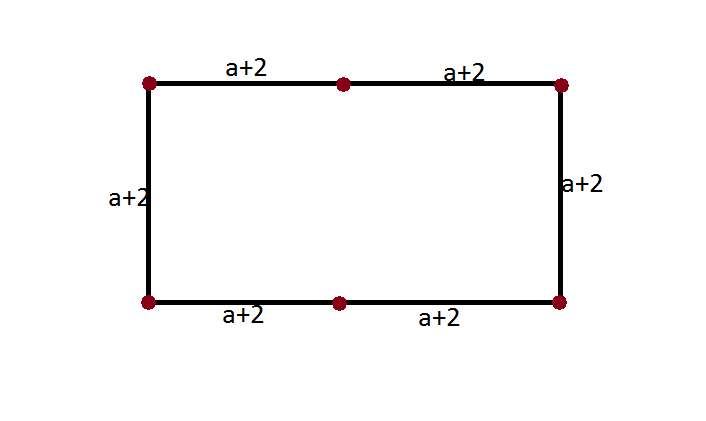
5---)) Kenar uzunlukları ( a+2) ve (2a+4) br olan , dikdörtgen şeklindeki bir bahçenin etrafına köşeleride dahil olmak üzere , eşit aralıklarla ağaç dikilecektir . En az kaç ağaç gerekir ?