lim
x→5
lim
x→-4
lim
x→5(soldan)
lim
x→5(sağdan)
1)Soruda limit verilen değer kritik nokta belirtmediğinden yerine yazarsak 25.sin(1/5)
2)Soruda verilen değer yerine yazıldığında kritik nokta elde ederiz. Bir fonksiyonun kritik noktalarında limit soruluyorsa, bu noktalarda sağdan ve soldan limite bakılır.Yani
sağdan x+4=-4+4=0
soldan -4-x=-4-(-4)=0 olacağından limitler sağdan ve soldan eşittir. Bu durumda limit 0 olacaktır.Bunu grafik ile de ispat edebiliriz.
f(x)=|x+4| ün grafiği;

Görüldüğü gibi grafikte -4 ün sağdan ve soldan limiti 0 olacaktır.
2)Soruda verilen değer yerine yazıldığında kritik nokta elde ederiz. Bir fonksiyonun kritik noktalarında limit soruluyorsa, bu noktalarda sağdan ve soldan limite bakılır.Yani
sağdan x+4=-4+4=0
soldan -4-x=-4-(-4)=0 olacağından limitler sağdan ve soldan eşittir. Bu durumda limit 0 olacaktır.Bunu grafik ile de ispat edebiliriz.
f(x)=|x+4| ün grafiği;
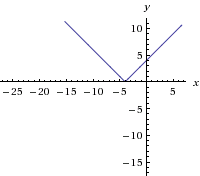
Görüldüğü gibi grafikte -4 ün sağdan ve soldan limiti 0 olacaktır.
3)  için ilk olarak 5 değerini x yerine yazdığımızda; e5-/(5--5)3=e5-/(0-)3 olacaktır burada;
için ilk olarak 5 değerini x yerine yazdığımızda; e5-/(5--5)3=e5-/(0-)3 olacaktır burada;
e5-/(0-)3= e5-.(-∞) olacaktır.(1/0-=-∞ olduğu için)
Bu durumda limit değerimiz;

olacaktır.
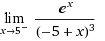 için ilk olarak 5 değerini x yerine yazdığımızda; e5-/(5--5)3=e5-/(0-)3 olacaktır burada;
için ilk olarak 5 değerini x yerine yazdığımızda; e5-/(5--5)3=e5-/(0-)3 olacaktır burada;e5-/(0-)3= e5-.(-∞) olacaktır.(1/0-=-∞ olduğu için)
Bu durumda limit değerimiz;

olacaktır.
4)Burada limit değerini limitin içindeki ln i limitin dışına çıkarabiliriz.
 Limit değerini bulmak için x yerine 5 yazarsak limit 0 bulunur. ln0 değerini bulabilmek için; ex=0 değerini bulmamız gereklidir. Bir üslü sayının 0 a eşit olabilmesi için üssünü -∞ olması gerektiğinden;
Limit değerini bulmak için x yerine 5 yazarsak limit 0 bulunur. ln0 değerini bulabilmek için; ex=0 değerini bulmamız gereklidir. Bir üslü sayının 0 a eşit olabilmesi için üssünü -∞ olması gerektiğinden;
x=-∞ olacaktır. Yani limit değerimiz -∞ dur.
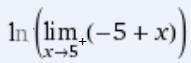 Limit değerini bulmak için x yerine 5 yazarsak limit 0 bulunur. ln0 değerini bulabilmek için; ex=0 değerini bulmamız gereklidir. Bir üslü sayının 0 a eşit olabilmesi için üssünü -∞ olması gerektiğinden;
Limit değerini bulmak için x yerine 5 yazarsak limit 0 bulunur. ln0 değerini bulabilmek için; ex=0 değerini bulmamız gereklidir. Bir üslü sayının 0 a eşit olabilmesi için üssünü -∞ olması gerektiğinden;x=-∞ olacaktır. Yani limit değerimiz -∞ dur.
Birinci soruyu x 0'a giderken olarak çözebilir miyiz rica etsem?

Teşekkür ederim cevaplarınız için 
Rica ederim.
