s(A)=m , s(B)=n olmak üzere A ->B tanımlanan
a) bağıntı sayısı ; 2m.n
b) fonksiyon sayısı ; nm
c) birebir fonksiyon sayısı ; P(n,m)= n! / (n-m)! (n≥m olmak şartıyla)
d) sabit fonksiyon sayısı ; n
e) birebir ve örten fonksiyon sayısı ; n! (n=m)
f) örten fonksiyon sayısı (m≥n)

Not: (n,k) büyük parantezi kombinasyondur. f şıkkının ispatı Matematik Dünyası dergisi 2003 I sayısından bakabilirsiniz.
Konu ile ilgili ayrıntılı dökümanı indirebilirsiniz. Gideceğiniz sayfada Dosya > Orjinalini İndir'e tıklayınız. link
Diğer indirme linki . İndirmek için gideceğiniz sayfada sağ tarafta "Karşıdan Yükle" linkine tıklayınız
a) bağıntı sayısı ; 2m.n
b) fonksiyon sayısı ; nm
c) birebir fonksiyon sayısı ; P(n,m)= n! / (n-m)! (n≥m olmak şartıyla)
d) sabit fonksiyon sayısı ; n
e) birebir ve örten fonksiyon sayısı ; n! (n=m)
f) örten fonksiyon sayısı (m≥n)
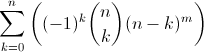
Not: (n,k) büyük parantezi kombinasyondur. f şıkkının ispatı Matematik Dünyası dergisi 2003 I sayısından bakabilirsiniz.
Konu ile ilgili ayrıntılı dökümanı indirebilirsiniz. Gideceğiniz sayfada Dosya > Orjinalini İndir'e tıklayınız. link
Diğer indirme linki . İndirmek için gideceğiniz sayfada sağ tarafta "Karşıdan Yükle" linkine tıklayınız
erken kalkan yol aır hemen başlayalım o zaman
s(A)=m , s(B)=n olsun
A→B
a) s(AxB)=m.n olacağından ve bu kümenin her bir altkümesi de bir bağıntı olacağından
toplam bağıntı sayısı = 2m.n olur
b) bir bağıntının fonksiyon olması için tanım kümesindeki tüm elemanların bir ve yalnız bir değer alması gerekir yani A daki her eleman B den tek bir elemene gitmelidir
A kümesinin her elemanı için B kümesinden n tane seçenek vardır
öyleyse toplam fonksiyon sayısı =n.n...n=nm olur
c) birebir fonksiyon olmak için A kümesndeki her elemanın B kümesindeki farklı bir elemana gitmesi gerekir. ilk eleman için n seçenek vardır ama 2. elema için artık (n-1) seçenek kalmışır, 3. eleman için (n-2) seçenek kalmıştır , ... , m. eleman için de (n-m+1)
sonuçta birebir fonksiyon sayısı=n.(n-1).(n-2)...(n-m+1)=n!/(n-m)! ya da P(n,m) olarak bulunur.
*işlemin doğası gereği B kümsini eleman sayısının en az A kümesinin eleman sayısı kadar olması gerektiğini de gördük.
d) sabit fonksiyon olmak için A kümesindeki her elemanın B kümesindeki aynı elemana gitmesi gerekir. ilk eleman için n tane seçenek vardır. ilk elemanın değeri belirlendikten sonra artık her eleman o değere gitmek zorunda olacağından toplam sabit fonksiyon sayısı
=n olur
e) birebir ve örten fonksiyon olmak için B deki her elemana A dan yalnız bir eleman gelmelidir ve B de açıkta eleman da kalmamalıdır. (s(A)=s(B)=m=n olması gerektiği doğal bir mantığın sonucu oluyor)
A daki ilk eleman için n seçenek vardır , sonraki eleman için (n-1) , ... , son eleman içinse tek seçenek
toplam birebir ve örten fonk. sayısı = n.(n-1).(n-2)...2.1=n! bulunur.
s(A)=m , s(B)=n olsun
A→B
a) s(AxB)=m.n olacağından ve bu kümenin her bir altkümesi de bir bağıntı olacağından
toplam bağıntı sayısı = 2m.n olur
b) bir bağıntının fonksiyon olması için tanım kümesindeki tüm elemanların bir ve yalnız bir değer alması gerekir yani A daki her eleman B den tek bir elemene gitmelidir
A kümesinin her elemanı için B kümesinden n tane seçenek vardır
öyleyse toplam fonksiyon sayısı =n.n...n=nm olur
c) birebir fonksiyon olmak için A kümesndeki her elemanın B kümesindeki farklı bir elemana gitmesi gerekir. ilk eleman için n seçenek vardır ama 2. elema için artık (n-1) seçenek kalmışır, 3. eleman için (n-2) seçenek kalmıştır , ... , m. eleman için de (n-m+1)
sonuçta birebir fonksiyon sayısı=n.(n-1).(n-2)...(n-m+1)=n!/(n-m)! ya da P(n,m) olarak bulunur.
*işlemin doğası gereği B kümsini eleman sayısının en az A kümesinin eleman sayısı kadar olması gerektiğini de gördük.
d) sabit fonksiyon olmak için A kümesindeki her elemanın B kümesindeki aynı elemana gitmesi gerekir. ilk eleman için n tane seçenek vardır. ilk elemanın değeri belirlendikten sonra artık her eleman o değere gitmek zorunda olacağından toplam sabit fonksiyon sayısı
=n olur
e) birebir ve örten fonksiyon olmak için B deki her elemana A dan yalnız bir eleman gelmelidir ve B de açıkta eleman da kalmamalıdır. (s(A)=s(B)=m=n olması gerektiği doğal bir mantığın sonucu oluyor)
A daki ilk eleman için n seçenek vardır , sonraki eleman için (n-1) , ... , son eleman içinse tek seçenek
toplam birebir ve örten fonk. sayısı = n.(n-1).(n-2)...2.1=n! bulunur.
ÖRNEK 1:
A ve B kümeleri için
s(A)=4 ve s(B)=2 olduğuna göre, A'dan B'ye kaç değişik bağıntı tanımlanabilir. ?
ÇÖZÜM 1:
s(AxB)=s(A).s(B)=4.2=8'dir.
AxB, 8 elemanlı bir küme olduğundan 28=256 tane alt kümesi vardır. AxB'nin herbir alt kümesi A dan B'ye tanımlı bir bağıntı olduğu için A→B'ye 256 bağıntı tanımlanabilir.
A ve B kümeleri için
s(A)=4 ve s(B)=2 olduğuna göre, A'dan B'ye kaç değişik bağıntı tanımlanabilir. ?
ÇÖZÜM 1:
s(AxB)=s(A).s(B)=4.2=8'dir.
AxB, 8 elemanlı bir küme olduğundan 28=256 tane alt kümesi vardır. AxB'nin herbir alt kümesi A dan B'ye tanımlı bir bağıntı olduğu için A→B'ye 256 bağıntı tanımlanabilir.
ÖRNEK 2:
s(A)=3 ve s(B)=4 olduğuna göre,
a) A→B'ye tanımlanacak bağıntı sayısını
b) A→B'ye tanımlanacak fonksiyon sayısını
c) A→B'ye tanımlanacak birebir fonksiyon sayısını
d) Sabit fonksiyon sayısını
bulunuz.
ÇÖZÜM 2:
a) 23.4=212
b) 4³=64
d) sabit fonksiyon sayısı 4 olur.
s(A)=3 ve s(B)=4 olduğuna göre,
a) A→B'ye tanımlanacak bağıntı sayısını
b) A→B'ye tanımlanacak fonksiyon sayısını
c) A→B'ye tanımlanacak birebir fonksiyon sayısını
d) Sabit fonksiyon sayısını
bulunuz.
ÇÖZÜM 2:
a) 23.4=212
b) 4³=64
c)
4!
(4-3)!
=24
d) sabit fonksiyon sayısı 4 olur.
Diğer çözümlü sorular alttadır.
