Soru 1: Çevresinin uzunluğu 27 cm olan bir ABC üçgeninde;
sinA+sinB=2.sinC
olduğuna göre |AB| kaç cm dir?
Soru 2:

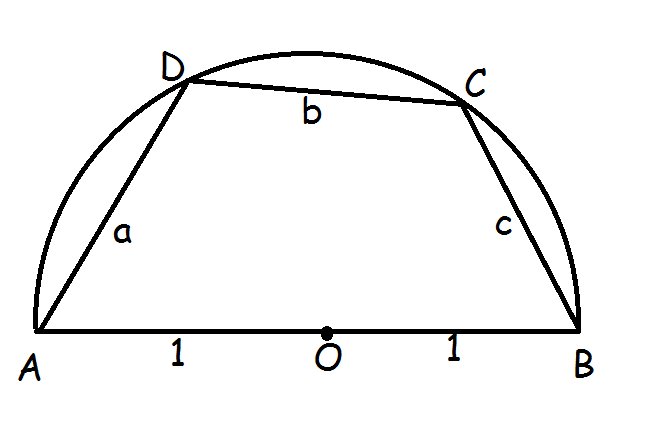
Şekildeki yarım çemberde;
a²+b²+c²+a.b.c=4 olduğunu gösteriniz.
Soru 3:

işleminin sonucu nedir?
sinA+sinB=2.sinC
olduğuna göre |AB| kaç cm dir?
Soru 2:
Şekildeki yarım çemberde;
a²+b²+c²+a.b.c=4 olduğunu gösteriniz.
Soru 3:
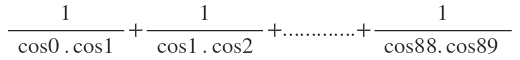
işleminin sonucu nedir?
3. sorunuz olimpiyat sorusu olabilir yanlış hatırlamıyorsam cevabıda galiba
cos1
sin21
3. sorunuz olimpiyat sorusu olabilir yanlış hatırlamıyorsam cevabıda galiba
cos1
sin21
1.
kenarların onları gören açıların sinüsleriyle doğru orantılı olduğunu biliyoruz
k.sinA+k.sinB+k.sinC=27
k.2sinC+k.sinC=27 → k.sinC=|AB|=9
2.
DB yi birleştirdiğinizde oluşturduğunuz dik açıyla pisagor yazılırsa ve pisagorda DB² yi BCD üçgeninde cos teoremi kullanarak ifade ederseniz , cosBCD=-sinDBA=-a/2 olduğunu da kullandığınızda istenen bulunur
3.
ifadeyi sin1 ile çarpıp bölerseniz
sin1/(cosx.cos(x+1)) şeklindeki terimlere baktığımızda sin1=sin(x+1-x)=sin(x+1).cosx-cos(x+1).sinx olarak yazdığımızda
sin1/(cosx.cos(x+1))=
=[sin(x+1).cosx-cos(x+1).sinx]/(cosx.cos(x+1))
=[sin(x+1).cosx/(cosx.cos(x+1))]-[cos(x+1).sinx/(cosx.cos(x+1))]
=tan(x+1)-tanx , x=0 dan 88 e toplarsanız (başta çarpıp böldüğümüz sin1 i de unutmadan) hocamızın dediği çıkacaktır
kenarların onları gören açıların sinüsleriyle doğru orantılı olduğunu biliyoruz
k.sinA+k.sinB+k.sinC=27
k.2sinC+k.sinC=27 → k.sinC=|AB|=9
2.
DB yi birleştirdiğinizde oluşturduğunuz dik açıyla pisagor yazılırsa ve pisagorda DB² yi BCD üçgeninde cos teoremi kullanarak ifade ederseniz , cosBCD=-sinDBA=-a/2 olduğunu da kullandığınızda istenen bulunur
3.
ifadeyi sin1 ile çarpıp bölerseniz
sin1/(cosx.cos(x+1)) şeklindeki terimlere baktığımızda sin1=sin(x+1-x)=sin(x+1).cosx-cos(x+1).sinx olarak yazdığımızda
sin1/(cosx.cos(x+1))=
=[sin(x+1).cosx-cos(x+1).sinx]/(cosx.cos(x+1))
=[sin(x+1).cosx/(cosx.cos(x+1))]-[cos(x+1).sinx/(cosx.cos(x+1))]
=tan(x+1)-tanx , x=0 dan 88 e toplarsanız (başta çarpıp böldüğümüz sin1 i de unutmadan) hocamızın dediği çıkacaktır
1.
kenarların onları gören açıların sinüsleriyle doğru orantılı olduğunu biliyoruz
k.sinA+k.sinB+k.sinC=27
k.2sinC+k.sinC=27 → k.sinC=|AB|=9
2.
DB yi birleştirdiğinizde oluşturduğunuz dik açıyla pisagor yazılırsa ve pisagorda DB² yi BCD üçgeninde cos teoremi kullanarak ifade ederseniz , cosBCD=-sinDBA=-a/2 olduğunu da kullandığınızda istenen bulunur
3.
ifadeyi sin1 ile çarpıp bölerseniz
sin1/(cosx.cos(x+1)) şeklindeki terimlere baktığımızda sin1=sin(x+1-x)=sin(x+1).cosx-cos(x+1).sinx olarak yazdığımızda
sin1/(cosx.cos(x+1))=
=[sin(x+1).cosx-cos(x+1).sinx]/(cosx.cos(x+1))
=[sin(x+1).cosx/(cosx.cos(x+1))]-[cos(x+1).sinx/(cosx.cos(x+1))]
=tan(x+1)-tanx , x=0 dan 88 e toplarsanız (başta çarpıp böldüğümüz sin1 i de unutmadan) hocamızın dediği çıkacaktır
kenarların onları gören açıların sinüsleriyle doğru orantılı olduğunu biliyoruz
k.sinA+k.sinB+k.sinC=27
k.2sinC+k.sinC=27 → k.sinC=|AB|=9
2.
DB yi birleştirdiğinizde oluşturduğunuz dik açıyla pisagor yazılırsa ve pisagorda DB² yi BCD üçgeninde cos teoremi kullanarak ifade ederseniz , cosBCD=-sinDBA=-a/2 olduğunu da kullandığınızda istenen bulunur
3.
ifadeyi sin1 ile çarpıp bölerseniz
sin1/(cosx.cos(x+1)) şeklindeki terimlere baktığımızda sin1=sin(x+1-x)=sin(x+1).cosx-cos(x+1).sinx olarak yazdığımızda
sin1/(cosx.cos(x+1))=
=[sin(x+1).cosx-cos(x+1).sinx]/(cosx.cos(x+1))
=[sin(x+1).cosx/(cosx.cos(x+1))]-[cos(x+1).sinx/(cosx.cos(x+1))]
=tan(x+1)-tanx , x=0 dan 88 e toplarsanız (başta çarpıp böldüğümüz sin1 i de unutmadan) hocamızın dediği çıkacaktır
