İntegral konusu ile ilgili 5 sorum var bakabilirmisiniz ?

Resim olarak eklediğim soruları çözemedim soruların cevaplarıda olmadığı için yaptıklarımın doğrumu yanlışmı olduğunuda bilemiyorum yardımcı olacağınızı düşünerek burada paylaşım yaptım şimdiden yardımı dokunan arkadaşlara ve hocalarımıza çok teşekkürler iyi günler.

1. sorunuz eksik.

2. soru:
V = ∏.(4-x²+2x)²-(4-x)² dx (0 ila 3) integrali çözülürse 153/5 ∏ bulunur.

Diğerleri için vakit bulursam yazarım.

teşekkürler yardımlarınız için diğer sorular ile ilgili çözümlerinizi de bekliyorum tekrar teşekkürler

Rica ederim.

3. soru:
Her t∈[0,2∏] için x '(t)=3cost ve y '(t)=-3sint olduğundan,

L=∫√[(3cost)²+(-3sint)²] dt (0 to 2∏) integrali çözülürse,

=|3|∫dt (0 to 2∏)

=6∏ olarak bulunur.


4. soru:
Her a∈[0,∏/2] için x '(a)=-3cos²a.sina ve y '(a)=3sin²α.cosα

x '(t)²+y '(t)²=9sin²α.cos²α olur.


S=Alan=2∏ ∫ y(a).√[x '(a)²+y '(a)²] da (0 to ∏/2) ; x-ekseninde dönüyor

S=Alan=2∏ .3.∫ sin⁴α.cosα dα (0 to ∏/2) çözülürse, (işlem hatası yapmadıysam) 6∏/5 bulunur.

cem hocam gerçekten çok teşekkürler yardımlarınız için acaba vaktiniz varsa son olarak şu sorulara da bakabilirmisiniz teşekkürler şimdiden

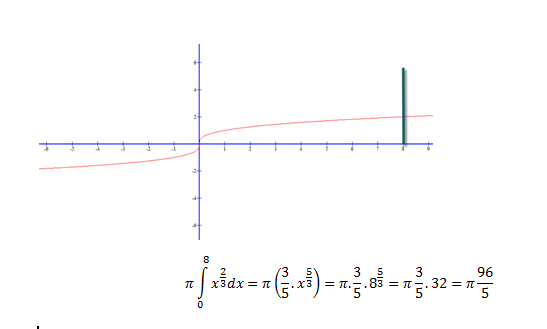
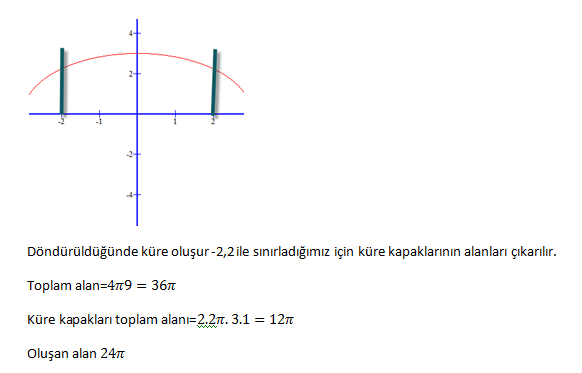
2

teşekkürler cevaplarınız için

Bu çözüm kabul etmezler, integral ile isterler sonucu.

Şöyle:
y=√9-x² --> y'=-x/√9-x²


S=2∏∫ |y|.√(1+(y')²) dx (-2 ila 2)
S=2∏∫√9-x².3/√9-x² dx (-2 ila 2)
S=2∏3 ∫dx (-2 ila 2)
S=6∏(2-8-2))
S=24∏

3. ve 5. sorular yine eksik: 3'de aralık vermeli ve 5'de de yoğunluk vermeli.

4. soru:
A=Alan=∫2sin2xdx (0 ila pi/2)=2

M_y=2∫x.sin2xdx (0 ila pi/2) çözülürse sanırım ∏³.sin2/12

M_x=1/2. ∫(2sin2x)²dx (0 ila pi/2) çözülürse pi/2

Ve ağırlık (kütle) merkezi;

x=M_y/A = ∏³sin2/24 ≈ 1,17

y=M_x/A = ∏/4 ≈0,78