1

2

3

4

2
3
4
C.1
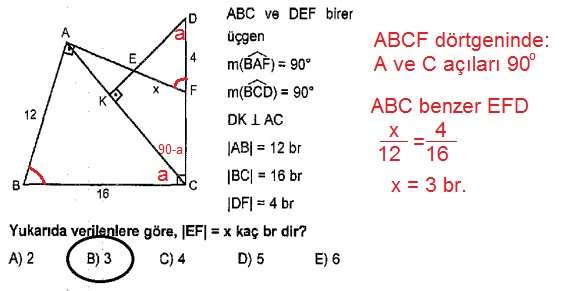
m(BAF)+m(BCD)=180 olduğundan ABCF dörtgeninin iç açıları toplamından;
m(ABC)+m(AFC)=180 olur.
m(DFA)+m(AFC)=180 olduğundan şöyle bir sonuç çıkarabiliriz:
m(ABC)=m(DFA).................................1
m(ACB)+m(DCK)=90 'dır.
CKD üçgeninin iç açılar toplamından;
m(CDK)+m(DCK)=90 olur.
Buradan; m(ACB)=m(CDK)....................2
Sonuç: 1 ve 2 numaralı eşitliklere göre DEF üçgeni ile ABC üçgenin tüm açıları eşittir. Dolayısıyla bu iki üçgen benzerdir. Benzerlik oranı:
4/16=x/12 => x=3 br bulunur.
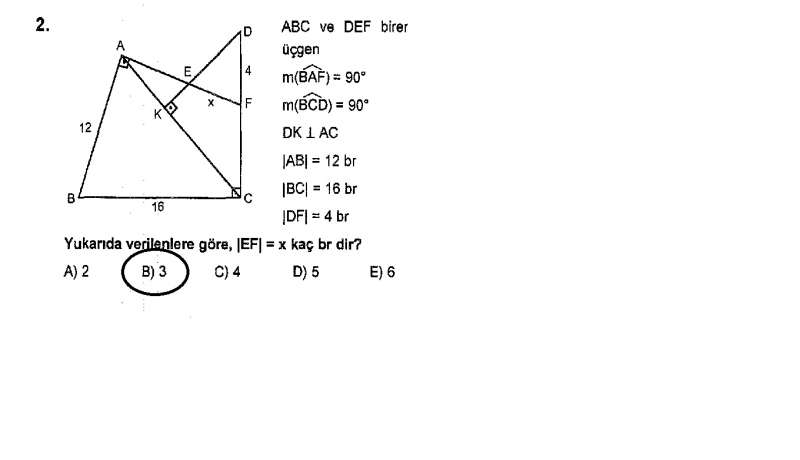
m(BAF)+m(BCD)=180 olduğundan ABCF dörtgeninin iç açıları toplamından;
m(ABC)+m(AFC)=180 olur.
m(DFA)+m(AFC)=180 olduğundan şöyle bir sonuç çıkarabiliriz:
m(ABC)=m(DFA).................................1
m(ACB)+m(DCK)=90 'dır.
CKD üçgeninin iç açılar toplamından;
m(CDK)+m(DCK)=90 olur.
Buradan; m(ACB)=m(CDK)....................2
Sonuç: 1 ve 2 numaralı eşitliklere göre DEF üçgeni ile ABC üçgenin tüm açıları eşittir. Dolayısıyla bu iki üçgen benzerdir. Benzerlik oranı:
4/16=x/12 => x=3 br bulunur.
C.2
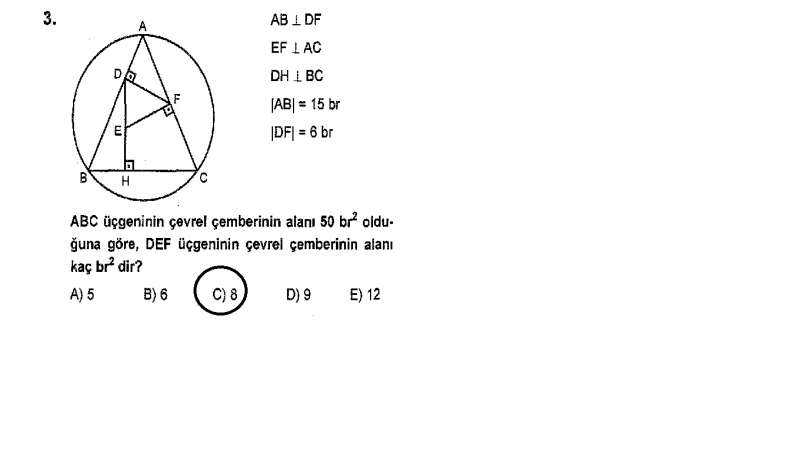
Açılar yazılırsa m(ACB)=m(DEF) bulunur.
m(ACB)=m(DEF)=β, ABC üçgeninin çevrel çemberinin yarıçapı m, DEF üçgeninin çevrel çemberinin yarıçapı n olsun. Çevrel çember alanları pi.m² ve pi.n² olur.
Sinüs teoreminden;
15/sin(β)=m
6/sin(β)=n=2m/5 olur.
pi.m²=50 br² ise pi.4m²/25=8 br² olur.
Açılar yazılırsa m(ACB)=m(DEF) bulunur.
m(ACB)=m(DEF)=β, ABC üçgeninin çevrel çemberinin yarıçapı m, DEF üçgeninin çevrel çemberinin yarıçapı n olsun. Çevrel çember alanları pi.m² ve pi.n² olur.
Sinüs teoreminden;
15/sin(β)=m
6/sin(β)=n=2m/5 olur.
pi.m²=50 br² ise pi.4m²/25=8 br² olur.
C.3

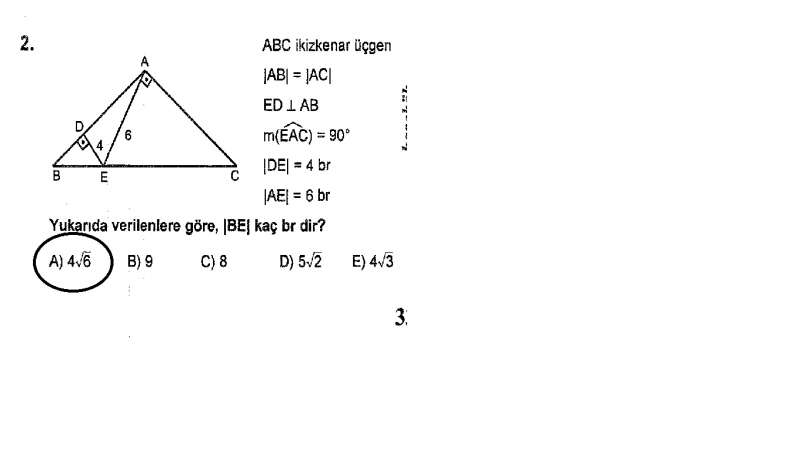
Daha sonra istenilen kenar uzunluğunu pisagordan 4√6 buluruz.
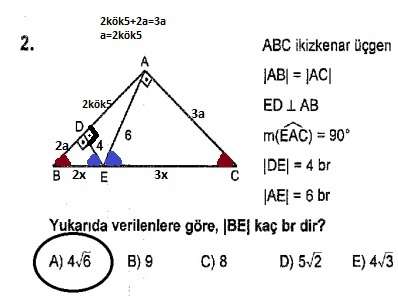
Daha sonra istenilen kenar uzunluğunu pisagordan 4√6 buluruz.
C.4
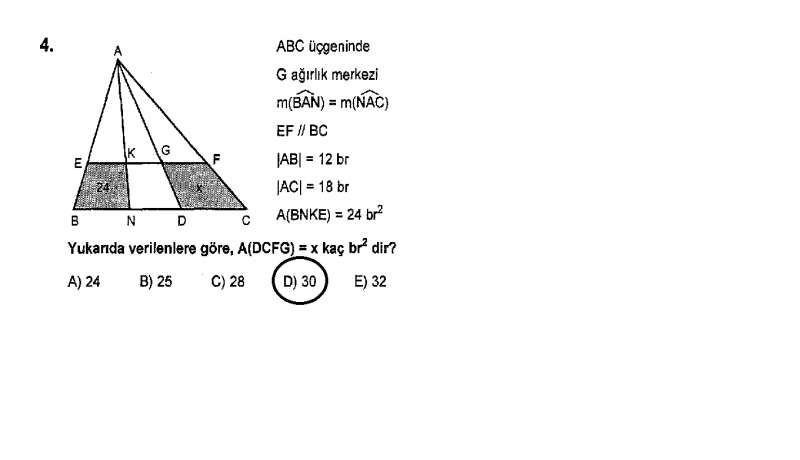
Ağırlık merkezinin özelliğinden |AG|/|AD|=2/3 olur. Paralellikten dolayı benzerlik yaparsak; A(ABN)=216/5 buluruz.
Açıortay teoreminden;
A(ABN)/A(ANC)=12/18=2/3 'dür. Buradan; A(ANC)=324/5 olur.
A(AND)=S olsun. Ağırlık merkezinin özelliğinden; A(ADC)=S+216/5 olur. Buradan;
2S+216/5=324/5 olur.
S=54/5 olur. Dolayısıyla; A(ADC)=54/5+216/5=270/5=54 olur. Orada da 2/3 benzerlik oranını (yani 4/9 alanlar oranını) uygularsak; x=(54/9).5=30 olur.
Ağırlık merkezinin özelliğinden |AG|/|AD|=2/3 olur. Paralellikten dolayı benzerlik yaparsak; A(ABN)=216/5 buluruz.
Açıortay teoreminden;
A(ABN)/A(ANC)=12/18=2/3 'dür. Buradan; A(ANC)=324/5 olur.
A(AND)=S olsun. Ağırlık merkezinin özelliğinden; A(ADC)=S+216/5 olur. Buradan;
2S+216/5=324/5 olur.
S=54/5 olur. Dolayısıyla; A(ADC)=54/5+216/5=270/5=54 olur. Orada da 2/3 benzerlik oranını (yani 4/9 alanlar oranını) uygularsak; x=(54/9).5=30 olur.
C.2
Açılar yazılırsa m(ABC)=m(DEF) bulunur.
m(ABC)=m(DEF)=β, ABC üçgeninin çevrel çemberinin yarıçapı m, DEF üçgeninin çevrel çemberinin yarıçapı n olsun. Çevrel çember alanları pi.m² ve pi.n² olur.
Sinüs teoreminden;
15/sin(β)=m
6/sin(β)=n=2m/5 olur.
pi.m²=50 br² ise pi.4m²/25=8 br² olur.
Açılar yazılırsa m(ABC)=m(DEF) bulunur.
m(ABC)=m(DEF)=β, ABC üçgeninin çevrel çemberinin yarıçapı m, DEF üçgeninin çevrel çemberinin yarıçapı n olsun. Çevrel çember alanları pi.m² ve pi.n² olur.
Sinüs teoreminden;
15/sin(β)=m
6/sin(β)=n=2m/5 olur.
pi.m²=50 br² ise pi.4m²/25=8 br² olur.
Birşey değil, teşekkür ederim. 
Tebrikler ''Mat.'' diğer soruları da neden 3 soru gibi çözmedin.
İnsan roman okur gibi oluyor.
Alternatif istekleri yerine getireyim.
1)

İnsan roman okur gibi oluyor.
Alternatif istekleri yerine getireyim.
1)