olasılık

3. soru yanlış; 25/36 olacak

evet hocam bu soru forumda çözüldü. galiba matematikçifm hocamız sormuştu geçmişimde kalan 3 soru diye. ayrıca cevabın 11/36 olması gerekir, siz diğer alanı hesaplamışsınız.

Evet evet değili olacak, ben düzünü yazmışım. 11/36

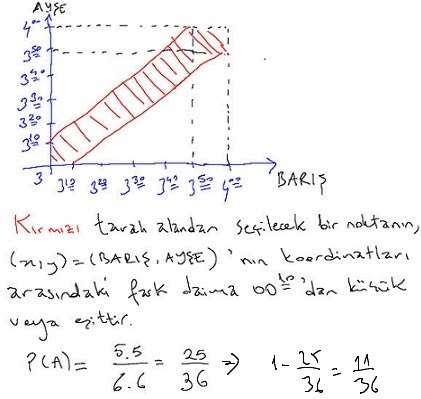
Onun yanlış olduğunu sonradan sezdim. 3.01,3.11 aralıkları da var sanırım oradan 50 durum oluşuyor yanılıyor muyum?

zaman dilimlerini ufaltarak sadece 11/36 ya daha yakın değerler elde edersin. limitin de 11/36 işte.

galiba 2. sorunuz da cevaplanmamış
nasıl bi cevap aranıyor belirtirseniz bişeyler uydurabiliriz gibime geliyor. biraz kağıt karaladım bişeyler buldum ama bu bulunan nasıl ifade edilmeli buna soru karar vermeli bence (tabi doğru bulmuşsam )

soruyu aynen byle vermiş hocamz ya baska bir açıklama vermemiş:s

Hatırladım bu soruyu. Ama hala, olasılık-zaman sorularını alan yardımı ile çözülmesini anlamış değilim.
Aklıma yatmayan şeyler var.

Evet Sayın Yorumcu o kalmış. Şöyle olmalı:

A, B den bağımsız olsun. E=B∪B' ve
A=A∩E --> P olasılık fonksiyonunu uygulayalım her iki tarafa;
P(A)=P(A∩E)
P(A)=P(A∩(B∪B'))=P((A∩B)∪(A∩B')) ; A∩B ve A∩B' olayları ayrık,
P(A)=P(A∩B)+P(A∩B')
P(A)=P(A\B')+P(A\B) yazılabilir.

Anlaşılıyor ki; A, B' den de bağımsız olabilir. Bu şartlar altında eşitlik yazılabilir.

ben de nasılsa sadece 2 olay var diye şöyle düşünmüştüm arkadaşımız artık hangisi kolayına gelirse onu uygulasın

A ve B için Venn şeması çizdim
A\B ye a , A∩B ye c , B\A ya b ve hepsinin dışında kalan yere de d yazdım

böylece verilen denklem
=P(A|B)+P(A|B')
=P(A∩B)/P(B)+P(A∩B')/P(B')
=(c/(b+c))+(a/(a+d)) olur ve bunun P(A) olduğu yani (a+c)/(a+b+c+d) olduğu verilmiş

bu denklem çarpılıp sadeleştirilip şu sonuca varılıyor
a(b+c)²+c(a+d)²=0 , burada iki terimin de 0 olması gerekli
b+c ve a+d 0 olamayacağına göre (koşullu olasılık tanımına uymaz)
a=c=0 bulunur (ayrıca b ve d nin 0 dan büyük olduğunun da belirtilmesi gerekli)
yani P(A)=0 ,
ya ilk çözdüğümde bunu göremedim ya da şimdi yazarken farklı bişeyler buldum böyle bulmamıştım diye hatırlıyorum