korkmazserkan 16:56 27 Ağu 2011 #1 
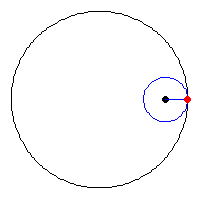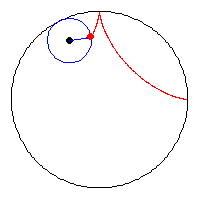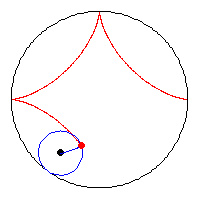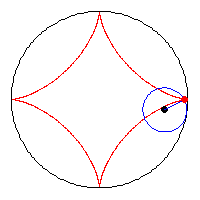
linkteki soruda Büyük bir çemberin içerisinde küçük bir çember var.
Bu küçük çember , büyük çemberin sınırlarına bitişik halde yuvarlanarak hareket ediyor.Ve hareketi sonlandığında çemberi 5 parçaya bölüyor
Küçük çemberin yarıçapı 2 ise ;
A-Parçalara ayrılmış büyük çemberin ortasında kalan büyük alan ne kadardır?
B-Parçalara ayrılmış büyük çemberin kenarlarında oluşan 4 eş parçadan birinin alanı ne kadardır?
C-Büyük çemberin yarıçapı ne kadardır?
D-Büyük çemberin Çevresi ne kadardır?
E-Büyük çemberin alanı ne kadardır? (∏=3)
korkmazserkan 13:26 28 Ağu 2011 #2
ilgilnen yok herhalde
ödev olunca kendin uğraşsan ii olacakk
gereksizyorumcu 05:04 29 Ağu 2011 #4
küçük çemberin 4 turunun tam olarak büyük çemberin 1 turuna karşılık geldiğini sanırım şekilden görebiliyoruz 
C-Büyük çemberin yarıçapı küçük çemberin yarıçapının 4 katıdır , R=8
D-çevre = 2∏R = 16∏
E-alan=∏R² = 64∏
şimdi o baklava dilimi benzeri şeklin nasıl oluştuğuna bakalım
buradan siyah noktanın (benim çizdiğim şekildeki siyah nokta)
x koordinatı x=3cost-sin(270-3t)=3cost+cos(3t)
y koordinatı da y=3sint+cos(270-3t)=3sint-sin(3t)
sin(3t)=3sint-4sin³t ve cos3t=4cos³t-3cost olduğunu biliyoruz öyleyse
parametrik denklemi
x=4sin³t , y=4cos³t olan bir eğrimiz vardır
bu eğrinin kapladığı alanı ∫ydx intgralini alarak bulabiliriz
1. bölgedeki alan için integral alınırsa sonuç 3∏/32 çıkıyor
yani tüm alan bunun 4 katıdır 12∏/32
ayrıca ben integralde büyük çemberin yarıçapının 1 olduğunu varsaydım. 8²=64 ile de çarpıp şeklimizi 8 kat büyüttüğümüzü düşünürsek sorulan alan
64.12∏/32=24∏ bulunur.
A-24∏
B-(64∏-24∏)/4=10∏
şeklin literatürdeki adı astroid
not:lütfen sorularınızda ∏=3 alınız yazmayınız. düzgün altıgen çizerek bile ∏ sayısının 3 ten büyük olduğunu görebiliyoruz ∏=∏
C-Büyük çemberin yarıçapı küçük çemberin yarıçapının 4 katıdır , R=8
D-çevre = 2∏R = 16∏
E-alan=∏R² = 64∏
şimdi o baklava dilimi benzeri şeklin nasıl oluştuğuna bakalım
buradan siyah noktanın (benim çizdiğim şekildeki siyah nokta)
x koordinatı x=3cost-sin(270-3t)=3cost+cos(3t)
y koordinatı da y=3sint+cos(270-3t)=3sint-sin(3t)
sin(3t)=3sint-4sin³t ve cos3t=4cos³t-3cost olduğunu biliyoruz öyleyse
parametrik denklemi
x=4sin³t , y=4cos³t olan bir eğrimiz vardır
bu eğrinin kapladığı alanı ∫ydx intgralini alarak bulabiliriz
1. bölgedeki alan için integral alınırsa sonuç 3∏/32 çıkıyor
yani tüm alan bunun 4 katıdır 12∏/32
ayrıca ben integralde büyük çemberin yarıçapının 1 olduğunu varsaydım. 8²=64 ile de çarpıp şeklimizi 8 kat büyüttüğümüzü düşünürsek sorulan alan
64.12∏/32=24∏ bulunur.
A-24∏
B-(64∏-24∏)/4=10∏
şeklin literatürdeki adı astroid
not:lütfen sorularınızda ∏=3 alınız yazmayınız. düzgün altıgen çizerek bile ∏ sayısının 3 ten büyük olduğunu görebiliyoruz ∏=∏
Hocam Elinize Sağlık Bayağı uğraşmısınız Serkan inşallah bu konuyla ilgili soru kaçırmazsın dershanede bile bu kadar ayrıntılı anlatmazlar
Serkan inşallah bu konuyla ilgili soru kaçırmazsın dershanede bile bu kadar ayrıntılı anlatmazlar gereksizyorumcu 05:29 29 Ağu 2011 #6
ayrıca yazmayı unutmuşum küçük çemberin yarıçapı büyüğün 1/4 ü kadar olduğundan büyük çemberdeki t birimlik açının ilerlemesi için küçüğün 4t kdar dönmesi gerekir. belirtilen açılar bu durumun sonucu olarak bulunmuştur.
gereksizyorumcu 05:30 29 Ağu 2011 #7 Hocam Elinize Sağlık Bayağı uğraşmısınız Serkan inşallah bu konuyla ilgili soru kaçırmazsın dershanede bile bu kadar ayrıntılı anlatmazlar
Serkan inşallah bu konuyla ilgili soru kaçırmazsın dershanede bile bu kadar ayrıntılı anlatmazlarböyle bi sorunun üniversite sınavında falan çıkmasını beklemiyosun heralde.
3.141592653589 09:48 29 Ağu 2011 #8
sanrım pi sayısını 3 almanın işlemden kaçmakdır.
3 veya 3.14 yerine 355/113 kesirini kullanmak çok daha hassas çözüme ulaştırır.
3 veya 3.14 yerine 355/113 kesirini kullanmak çok daha hassas çözüme ulaştırır.
korkmazserkan 12:33 29 Ağu 2011 #9
ben bu soruyu normal bir çember sorusu olarak düşünmüştüm ben basit gidecektim ama soruyu bide burda sorayım en doğru çözümü görmek istedim beni aşıyor