Bir bileşik önerme, kendisini oluşturan her değeri için daima doğru oluyorsa, bu
bileşik önermeye totoloji, daima yanlış oluyorsa, bu bileşik önermeye de çelişki denir.
Verilen p herhangi bir önerme için, p V p' ile p Λ q' bileşik önermelerinin
doğruluk değerleri tablosunu yapalım.
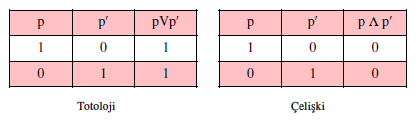
Tablodan, p V p' ≡ 1 ve p Λ p' ≡ 0 olduğu görülüyor. Buna göre, p V p' bileşik
önermesi bir totolojidir. p Λ p' önermesi ise bir çelişkidir.
bileşik önermeye totoloji, daima yanlış oluyorsa, bu bileşik önermeye de çelişki denir.
Verilen p herhangi bir önerme için, p V p' ile p Λ q' bileşik önermelerinin
doğruluk değerleri tablosunu yapalım.

Tablodan, p V p' ≡ 1 ve p Λ p' ≡ 0 olduğu görülüyor. Buna göre, p V p' bileşik
önermesi bir totolojidir. p Λ p' önermesi ise bir çelişkidir.
ÖRNEK:
(1⇔0)'⇔[(0⇒1)Λ1]
işleminin sonucunun totoloji mi çelişki mi olduğuna bakalım
ÇÖZÜM
Bu çözümde ancak ve ancak bağlacı özelliği kullanılacaktır.
(p⇒q)Λ(q⇒p)≡p⇔q özellik için bknz (Mantık Formülleri - Ve , Veya, İse, Ancak ve Ancak Özellikleri)
Bu bilgiye göre,
(1⇔0)'⇔[(0⇒1)Λ1]=0'⇔(1Λ1)≡1⇔1≡1 bulunur.
Cevap 1'e denk olduğundan totolojidir diyebiliriz.
(1⇔0)'⇔[(0⇒1)Λ1]
işleminin sonucunun totoloji mi çelişki mi olduğuna bakalım
ÇÖZÜM
Bu çözümde ancak ve ancak bağlacı özelliği kullanılacaktır.
(p⇒q)Λ(q⇒p)≡p⇔q özellik için bknz (Mantık Formülleri - Ve , Veya, İse, Ancak ve Ancak Özellikleri)
Bu bilgiye göre,
(1⇔0)'⇔[(0⇒1)Λ1]=0'⇔(1Λ1)≡1⇔1≡1 bulunur.
Cevap 1'e denk olduğundan totolojidir diyebiliriz.
Diğer çözümlü sorular alttadır.
