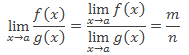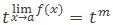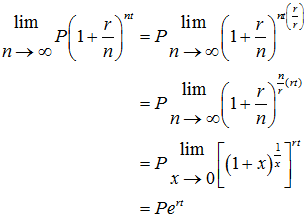m,n ∈ R velimx→af(x) = m,limx→ag(x) = n olmak üzere;
1.limx→a[f(x) ± g(x)] =limx→af(x) ±limx→ag(x) = m ± n
2.limx→a[f(x) . g(x)] =limx→af(x) .limx→ag(x) = m . n
3. n ≠ 0 olmak üzere;
4. k ∈ R olsun;
limx→ak.f(x) = k.limx→af(k) = k.m
5.limx→a|f(x)| = |limx→af(x)|
6. t ∈ R
limx→atf(x) =
7. P ∈ N⁺ = {1, 2, .....} olmak üzere;
m ≥ 0 ise;
limx→ap√f(x) = p√limx→af(x) = p√m
m < 0 ve p çift ise ;
limx→ap√f(x) mevcut değildir.
8. f sınırlı bir fonksiyon velimx→ag(x) = 0 ise;
limlx→af(x).g(x) = 0 dır. (Bu teoremin tersi doğru değildir.)
9. f,g,h fonksiyonları için, f(x) ≤ h(x) ≤ g(x) ve
limx→af(x) =limx→ag(x) = r ise;
limx→ah(x) = r dir.
10.limx→a[log(fx)] = log[limx→af(x)] = log(m); f(x) > 0
11.limx→a[f(x)]n = [limx→af(x)]n = mn, n ∈ N⁺
12. f(x) = P(x) şeklinde bir polinom ise;
limx→aP(x) = P(a)
13. a > 1, n ∈ N⁺, m > 1 olmak üzere x → ∞ iken;
xx > x! > ax > xn > logmx
14.limx→∞√ax²+bx+c = √a.limx→∞|x+b2a|, a>0
15.limx→0sinaxbx=ab
limx→0tanaxbx=ab
limx→0axtanbx=ab
limx→0axsinbx=ab
16.limx→0ax±b.sincxdx±e.sinfx=a±b.cd±e.fdir. a, b, c, d, e, f ∈ R
17.
18.limx→0xln(1±x)= ±1