svsmumcu26 22:59 23 Haz 2013 #1
Bazen alan hesabını yapmak çok zahmetli olur (2.dereceden kök hesabı,türev filan) şimdi bunlara hiç dokunmadan maksimum alan-kenar soru tiplerine farklı bir bakış getireceğiz.
Bir örnekle başlayalım.
Kenar uzunlukları 2x br , 4x br ve 12 br olan bir üçgenin alanı en çok kaç br² olabilir?
Çözüm I.
Aslında burada heron formülünden yerine yazıp türev bilgisiyle soruyu çözebiliriz.
Ama sizi zahmete sokmadan Apollon Çemberi yardımıyla bu soruya farklı bir çözüm getireceğiz.
II.Çözümü izleyin.
Çözüm II.(Apollon Çemberi)
ABC üçgenini inşaat etmeye çalışacağız boyu 12 br olan kenarı [BC] seçelim ve hemen [BC]'yi çizelim.
Şimdi A'nın nerelerde olabileceğini araştıracağız.Verilenlere göre |AB|=4x br ve |AC|=2x br yani A'nın B'ye olan uzaklığı C'ye olan uzaklığının 2 katı olacakmış.
Şimdi bu noktaları doğru üzerinde işaretleyelim bakalım.
Şimdi birkaç tane de göz kararı noktalar işaretleyelim.
Bu noktaların çembersel olduğunu anlamış olmanız lazım hatta [A₁A₂]nin de çap olduğunu da bir başka konuda kanıtlayacağım inşallah.
Şimdi çemberimizi hayali olarak oluşturalım bakalım.
ABC üçgeninin tabanı sabit olduğundan,alanı maksimum yapmak için yüksekliği olabilecek en büyük tutmalıyız.Peki hangi A noktası BC'ye en uzaktır? Çemberin en üst noktası olan A5 değil mi?
Onu da çizelim.
Şimdi hesaplayabiliriz taban 8+4 = 12 br , yükseklik 8 birim olduğundan alan
12.8/2 = 48 br² bulunur.
Bir örnekle başlayalım.
Kenar uzunlukları 2x br , 4x br ve 12 br olan bir üçgenin alanı en çok kaç br² olabilir?
Çözüm I.
Aslında burada heron formülünden yerine yazıp türev bilgisiyle soruyu çözebiliriz.
Ama sizi zahmete sokmadan Apollon Çemberi yardımıyla bu soruya farklı bir çözüm getireceğiz.
II.Çözümü izleyin.
Çözüm II.(Apollon Çemberi)
ABC üçgenini inşaat etmeye çalışacağız boyu 12 br olan kenarı [BC] seçelim ve hemen [BC]'yi çizelim.
Şimdi A'nın nerelerde olabileceğini araştıracağız.Verilenlere göre |AB|=4x br ve |AC|=2x br yani A'nın B'ye olan uzaklığı C'ye olan uzaklığının 2 katı olacakmış.
Şimdi bu noktaları doğru üzerinde işaretleyelim bakalım.
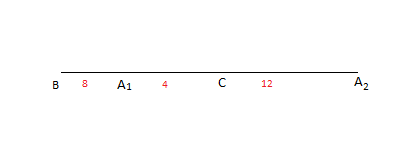
Şimdi birkaç tane de göz kararı noktalar işaretleyelim.
Bu noktaların çembersel olduğunu anlamış olmanız lazım hatta [A₁A₂]nin de çap olduğunu da bir başka konuda kanıtlayacağım inşallah.
Şimdi çemberimizi hayali olarak oluşturalım bakalım.
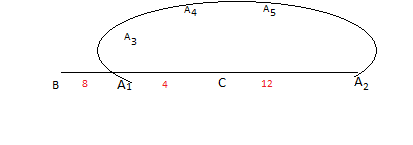
ABC üçgeninin tabanı sabit olduğundan,alanı maksimum yapmak için yüksekliği olabilecek en büyük tutmalıyız.Peki hangi A noktası BC'ye en uzaktır? Çemberin en üst noktası olan A5 değil mi?
Onu da çizelim.
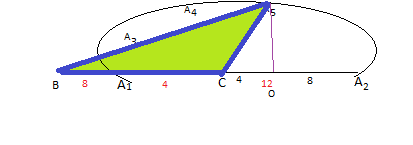
Şimdi hesaplayabiliriz taban 8+4 = 12 br , yükseklik 8 birim olduğundan alan
12.8/2 = 48 br² bulunur.
cengizhanhck 23:22 23 Haz 2013 #2
3.Yol (Türevle nasil yapiliyo bilmiyorum benziyo olabilir.)Parabolün tepe noktasindan veya tam kareye tamamlayip ikinci dereceden bir fonksiyonun maksimum değerini bulacağiz.
ALAN=a olsun a²=(3x+6)(x+6)(6-x)(3x-6) ayrica üçgen eşitsizliğinde 2<x<6 bu bir kösede kalsin
a²=9(x+6)(6-x)(x+2)(x-2)=(36-x²)(x²-4) x²-4=p olsun o halde 36-x²=-p+32 olur
burdan a²=p(-p+32)=-p²+32p burdanda p=16 için (tam kareye tamamlarsak veya parabolün tepe noktasi) maksimum değeri alir.Ayrica x²-4=p=16 için x=2√5 olur. 2√5<6 olduguna göre x=2√5 alabiliriz. a²=9(16)(16) a=3.4.4=48.
ALAN=a olsun a²=(3x+6)(x+6)(6-x)(3x-6) ayrica üçgen eşitsizliğinde 2<x<6 bu bir kösede kalsin
a²=9(x+6)(6-x)(x+2)(x-2)=(36-x²)(x²-4) x²-4=p olsun o halde 36-x²=-p+32 olur
burdan a²=p(-p+32)=-p²+32p burdanda p=16 için (tam kareye tamamlarsak veya parabolün tepe noktasi) maksimum değeri alir.Ayrica x²-4=p=16 için x=2√5 olur. 2√5<6 olduguna göre x=2√5 alabiliriz. a²=9(16)(16) a=3.4.4=48.
Adam
hiç
üşen
memiş
anlat
mış
ya
hu
hiç
üşen
memiş
anlat
mış
ya
hu
svsmumcu26 00:55 24 Haz 2013 #4 3.Yol (Türevle nasil yapiliyo bilmiyorum benziyo olabilir.)Parabolün tepe noktasindan veya tam kareye tamamlayip ikinci dereceden bir fonksiyonun maksimum değerini bulacağiz.
ALAN=a olsun a²=(3x+6)(x+6)(6-x)(3x-6) ayrica üçgen eşitsizliğinde 2<x<6 bu bir kösede kalsin
a²=9(x+6)(6-x)(x+2)(x-2)=(36-x²)(x²-4) x²-4=p olsun o halde 36-x²=-p+32 olur
burdan a²=p(-p+32)=-p²+32p burdanda p=16 için (tam kareye tamamlarsak veya parabolün tepe noktasi) maksimum değeri alir.Ayrica x²-4=p=16 için x=2√5 olur. 2√5<6 olduguna göre x=2√5 alabiliriz. a²=9(16)(16) a=3.4.4=48.
ALAN=a olsun a²=(3x+6)(x+6)(6-x)(3x-6) ayrica üçgen eşitsizliğinde 2<x<6 bu bir kösede kalsin
a²=9(x+6)(6-x)(x+2)(x-2)=(36-x²)(x²-4) x²-4=p olsun o halde 36-x²=-p+32 olur
burdan a²=p(-p+32)=-p²+32p burdanda p=16 için (tam kareye tamamlarsak veya parabolün tepe noktasi) maksimum değeri alir.Ayrica x²-4=p=16 için x=2√5 olur. 2√5<6 olduguna göre x=2√5 alabiliriz. a²=9(16)(16) a=3.4.4=48.
Heron formülünden yerine yazarsanız çıkıyor.
Adam
hiç
üşen
memiş
anlat
mış
ya
hu
hiç
üşen
memiş
anlat
mış
ya
hu
svsmumcu26 02:48 24 Haz 2013 #5
İlginç forumda Apollon çemberine hiç değinilmemiş.
gereksizyorumcu 12:34 24 Haz 2013 #6 İlginç forumda Apollon çemberine hiç değinilmemiş.
svsmumcu26 12:36 24 Haz 2013 #7 bu çemberin denklemi, nasıl oluştuğu vs gibi bilgileri de ilk mesajda belirtip altına "bakın böyle bir soruyu da hiç türeve girmeden çözebiliriz" diyerek yukardaki örneği verirsek daha iyi olur diye düşünüyorum.