Özellik1: Bir kenar uzunluğu ve diğer 2 kenarın uzunlukları toplamı yani bir kenarı ve çevresi belli olan bir üçgen verilmeyen diğer 2 kenar eşit olduğunda (ikizkenar olduğunda) maksimum alana ulaşır.
İspat1: Heron formülü
Üçgenin kenar uzunlukları a,b,c ve çevresi de p=2u=a+b+c olsun.
Heronun alan formülünü hatırlayalım

Burada a ve p=2u verilmiş ve sabittir , dolayısıyla u ve (u-a) sabittir. Alanın maksimum değerini alması için
(u-b).(u-c) nin en büyük değerini alması gereklidir
bu iki sayının toplamı sabit olduğuna göre de çarpımları en büyük değeri eşit olduklarında alır
(u-b)=(u-c) ve dolayısıyla b=c, en büyük alan için üçgenimiz ikizkenar olmalıymış.
İspat2: Geometrik yaklaşım
Üçgenin verilen kenarı |AB|=c olsun bu durumda tüm C noktaları odakları A ve B olan bir elips çizer (elips: sabit 2 noktadan-odaklardan uzaklıkları toplamı eşit olan noktalar kümesi)
Biz de bu elipsi çizelim.

C' elipsin küçük ekseninin üzerindedir.
eğer C noktası C' ile çakışık değilse yani b=c ya da üçgen ikizkenar değilse C noktasını C' noktasına kaydırdığımızda çevre değişmediği halde üçgenin yüksekliği ve dolayısıyla alanı artacaktır, sonuçta maksimum alan için üçgen ikizkenar olmalıdır.
İspat1: Heron formülü
Üçgenin kenar uzunlukları a,b,c ve çevresi de p=2u=a+b+c olsun.
Heronun alan formülünü hatırlayalım
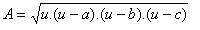
Burada a ve p=2u verilmiş ve sabittir , dolayısıyla u ve (u-a) sabittir. Alanın maksimum değerini alması için
(u-b).(u-c) nin en büyük değerini alması gereklidir
bu iki sayının toplamı sabit olduğuna göre de çarpımları en büyük değeri eşit olduklarında alır
(u-b)=(u-c) ve dolayısıyla b=c, en büyük alan için üçgenimiz ikizkenar olmalıymış.
İspat2: Geometrik yaklaşım
Üçgenin verilen kenarı |AB|=c olsun bu durumda tüm C noktaları odakları A ve B olan bir elips çizer (elips: sabit 2 noktadan-odaklardan uzaklıkları toplamı eşit olan noktalar kümesi)
Biz de bu elipsi çizelim.
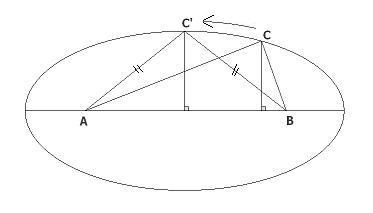
C' elipsin küçük ekseninin üzerindedir.
eğer C noktası C' ile çakışık değilse yani b=c ya da üçgen ikizkenar değilse C noktasını C' noktasına kaydırdığımızda çevre değişmediği halde üçgenin yüksekliği ve dolayısıyla alanı artacaktır, sonuçta maksimum alan için üçgen ikizkenar olmalıdır.
Özellik2: 2 kenarı verilen bir üçgende maksimum alana bu iki kenar dik olduğunda ulaşılır.
İspat: Verilen 2 kenar uzunluğu a ve b , aralarındaki açı da C olsun. Bu durumda sinüs teoremine göre alan
 olacağından ve a ile b verildiğinden maksimum alana sinC nin maksimum değerinde yani C dik açı olduğunda ulaşılır.
olacağından ve a ile b verildiğinden maksimum alana sinC nin maksimum değerinde yani C dik açı olduğunda ulaşılır.
Özellik3: Çevresi verilen üçgenler içinde en büyük alana sahip olanı eşkenar üçgendir.
İspat1: Heron formülü
Üçgenin kenar uzunlukları a,b,c ve çevresi de p=2u=a+b+c olsun.
Yine Heronun alan formülünden faydalanırsak

Çevre verildiğinden yarı çevre=u sabit olduğuna göre (u-a).(u-b).(u-c) çarpımının maksimum değerini alması gerekmektedir.
u-a=x , u-b=y , u-c=z dönüşümü yaptığımızda
x+y+z=u-a+u-b+u-c=3u-2u=u olacaktır.
Aritmetik Orta Geometrik Orta eşitsizliğinden

ise

olacaktır ve eşitlik ise sadece x=y=z yani (u-a)=(u-b)=(u-c) yani üçgen eşkenar olduğunda sağlanacaktır.
İspat2: Üçgenin C köşesinde birleşen ve eşit olmayan iki kenarı a ve b olsun. Diğer kenara bakılmaksızın bu 2 kenarın uzunlukları toplamı sabit düşünülüp ikizkenar hale getirildiğinde Özellik1e göre daha büyük bir alana ulaştığımızı görmüştük. Bunun sonucu olarak üçgende farklı uzunlukta 2 kenar varsa her zaman için alanı büyütebiliriz. Alan maksimum olacaksa a=b=c yani üçgen eşkenar olmalıdır.
İspat: Verilen 2 kenar uzunluğu a ve b , aralarındaki açı da C olsun. Bu durumda sinüs teoremine göre alan
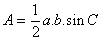 olacağından ve a ile b verildiğinden maksimum alana sinC nin maksimum değerinde yani C dik açı olduğunda ulaşılır.
olacağından ve a ile b verildiğinden maksimum alana sinC nin maksimum değerinde yani C dik açı olduğunda ulaşılır.Özellik3: Çevresi verilen üçgenler içinde en büyük alana sahip olanı eşkenar üçgendir.
İspat1: Heron formülü
Üçgenin kenar uzunlukları a,b,c ve çevresi de p=2u=a+b+c olsun.
Yine Heronun alan formülünden faydalanırsak
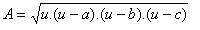
Çevre verildiğinden yarı çevre=u sabit olduğuna göre (u-a).(u-b).(u-c) çarpımının maksimum değerini alması gerekmektedir.
u-a=x , u-b=y , u-c=z dönüşümü yaptığımızda
x+y+z=u-a+u-b+u-c=3u-2u=u olacaktır.
Aritmetik Orta Geometrik Orta eşitsizliğinden
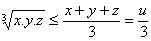
ise
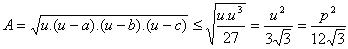
olacaktır ve eşitlik ise sadece x=y=z yani (u-a)=(u-b)=(u-c) yani üçgen eşkenar olduğunda sağlanacaktır.
İspat2: Üçgenin C köşesinde birleşen ve eşit olmayan iki kenarı a ve b olsun. Diğer kenara bakılmaksızın bu 2 kenarın uzunlukları toplamı sabit düşünülüp ikizkenar hale getirildiğinde Özellik1e göre daha büyük bir alana ulaştığımızı görmüştük. Bunun sonucu olarak üçgende farklı uzunlukta 2 kenar varsa her zaman için alanı büyütebiliriz. Alan maksimum olacaksa a=b=c yani üçgen eşkenar olmalıdır.
Özellik4: Çevresi verilen şekiller arasında en büyük alana sahip olan dairedir.
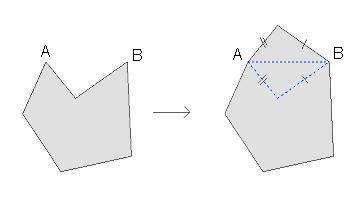
İspat: Öncelikle şeklimizin konveks olması gereklidir. Eğer şekil A ve B noktaları arasında konveks değilse bu iki nokta arasındaki kısmının AB ye göre simetriğinin aldığımızda çevre uzunluğunu değiştirmeden alanı artırmış oluruz ki bu maksimum alan olması durumuyla çelişir.

A ve B şeklimizin çevresini eşit uzunlukta 2 parçaya ayıran herhangi 2 nokta olsun.
Bu durumda AB doğru parçası da şeklimizin alanını 2 eşit parçaya ayırmak zorundadır. Aksi halde S1>S2 olduğunda şeklin S1 kısmının AB ye göre simetriğini aldığımızda aynı çevreyle daha büyük bir alana ulaşmış oluruz.

Şu an belli bir uzunluk ve sonsuz bir çizgi yardımıyla en büyük alanın o çizginin üzerine verilen uzunlukta bir yarım çember çizmek olduğunu göstermemiz yeterlidir.
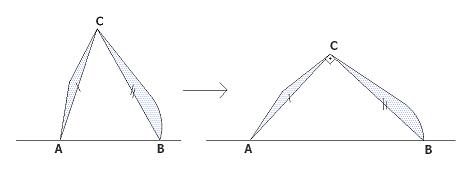
Bu yarı uzunluk A noktasından başlasın B noktasında bitsin. Bu parçanın üzerinde herhangi bi C noktası seçip A ve B ye birleştirelim. ACB açısı dik değilse Özellik2nin sonucu olarak dik açı haline getirdiğimizde verilen çevreyi değiştirmeden üçgenin alanını büyüttüğümüz için daha büyük bir toplam alana ulaşırız. Sonuçta maksimum alan oluştuğunda ACB açısı dik olmalıdır. C noktası herhangi bir nokta olacağından AB yi gören ve bu şeklin üzerinde C noktası gibi bir köşesi olan her açı da dik olmalıdır. Bu tür C noktaları ise çapı AB olan bir yarım çember çizerler.

Bu da çevresi verilen şekiller arasında en büyük alana sahip olanın daire olduğunu gösterir.
Özellik5: Çevresi verilen herhangi bir çokgende maksimum alan çokgen düzgün olduğunda elde edilir.
İspat: Çokgenin eşit olmayan iki komşu kenarı a ve b olsun. Bu durumda Özellik1e göre çokgenin çevresini değiştirmeden bu iki kenarı (a+b)/2 de eşitleyerek alanı büyütebiliriz. Bu işlemin sonucu olarak maksimum alana sahip olunduğunda farklı uzunluğa sahip 2 komşu kenar olmamalıdır yani çokgenin tüm kenarları eşit olmalıdır. Çokgenimizin tüm kenarlarının eşit olması düzgün olmasını gerektirmez aynı zamanda tüm açılarının da eşit olduğunu göstermeliyiz. Özellik4ün ispatındaki gibi bir uygulamayla bir yarıçevre belirleyip çokgenin köşelerini o yarıçevrenin uçlarına birleştirdiğimizde (kenar sayısı tekse 2 kenarın uzatılılıp kesiştiği noktaya birleştiririz) bu tür tüm açıların dik olması ve dolayısıyla yarıçevrenin bir tarafında kalan tüm köşelerin aynı yarım çember üzerinde ve sonucu olarak da çokgenin tüm köşelerinin aynı çember üzerinde olması gerektiğini buluruz. Kenarları eşit ve köşeleri aynı çember üzerindeyse bu bir düzgün çokgendir.
Siz de bu özellikten faydalanıp Özellik4ü farklı bir yoldan ispatlayabilirsiniz.
İspat: Öncelikle şeklimizin konveks olması gereklidir. Eğer şekil A ve B noktaları arasında konveks değilse bu iki nokta arasındaki kısmının AB ye göre simetriğinin aldığımızda çevre uzunluğunu değiştirmeden alanı artırmış oluruz ki bu maksimum alan olması durumuyla çelişir.
A ve B şeklimizin çevresini eşit uzunlukta 2 parçaya ayıran herhangi 2 nokta olsun.
Bu durumda AB doğru parçası da şeklimizin alanını 2 eşit parçaya ayırmak zorundadır. Aksi halde S1>S2 olduğunda şeklin S1 kısmının AB ye göre simetriğini aldığımızda aynı çevreyle daha büyük bir alana ulaşmış oluruz.
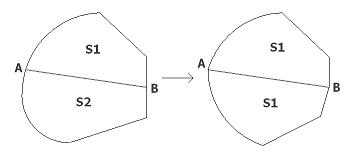
Şu an belli bir uzunluk ve sonsuz bir çizgi yardımıyla en büyük alanın o çizginin üzerine verilen uzunlukta bir yarım çember çizmek olduğunu göstermemiz yeterlidir.
Bu yarı uzunluk A noktasından başlasın B noktasında bitsin. Bu parçanın üzerinde herhangi bi C noktası seçip A ve B ye birleştirelim. ACB açısı dik değilse Özellik2nin sonucu olarak dik açı haline getirdiğimizde verilen çevreyi değiştirmeden üçgenin alanını büyüttüğümüz için daha büyük bir toplam alana ulaşırız. Sonuçta maksimum alan oluştuğunda ACB açısı dik olmalıdır. C noktası herhangi bir nokta olacağından AB yi gören ve bu şeklin üzerinde C noktası gibi bir köşesi olan her açı da dik olmalıdır. Bu tür C noktaları ise çapı AB olan bir yarım çember çizerler.
Bu da çevresi verilen şekiller arasında en büyük alana sahip olanın daire olduğunu gösterir.
Özellik5: Çevresi verilen herhangi bir çokgende maksimum alan çokgen düzgün olduğunda elde edilir.
İspat: Çokgenin eşit olmayan iki komşu kenarı a ve b olsun. Bu durumda Özellik1e göre çokgenin çevresini değiştirmeden bu iki kenarı (a+b)/2 de eşitleyerek alanı büyütebiliriz. Bu işlemin sonucu olarak maksimum alana sahip olunduğunda farklı uzunluğa sahip 2 komşu kenar olmamalıdır yani çokgenin tüm kenarları eşit olmalıdır. Çokgenimizin tüm kenarlarının eşit olması düzgün olmasını gerektirmez aynı zamanda tüm açılarının da eşit olduğunu göstermeliyiz. Özellik4ün ispatındaki gibi bir uygulamayla bir yarıçevre belirleyip çokgenin köşelerini o yarıçevrenin uçlarına birleştirdiğimizde (kenar sayısı tekse 2 kenarın uzatılılıp kesiştiği noktaya birleştiririz) bu tür tüm açıların dik olması ve dolayısıyla yarıçevrenin bir tarafında kalan tüm köşelerin aynı yarım çember üzerinde ve sonucu olarak da çokgenin tüm köşelerinin aynı çember üzerinde olması gerektiğini buluruz. Kenarları eşit ve köşeleri aynı çember üzerindeyse bu bir düzgün çokgendir.
Siz de bu özellikten faydalanıp Özellik4ü farklı bir yoldan ispatlayabilirsiniz.
Nasıl teşekkür etmemişim.
Eliniz dert görmesin Sabri hocam.
Eliniz dert görmesin Sabri hocam.
Diğer çözümlü sorular alttadır.
maksimum alan Maksimum Problemleri Matematik Teoremleri ve İspatları minimum çevre Türev Formülleri Türev Maksimum Minimum Problemleri
Tüm Etiketler
Tüm Etiketler
