
Çözmeye paydadan başlayalım, 4⁻¹=1/4 ve 1/m⁻¹=m olarak kullanalım çözümde,
(1/4)+m=(4m+1)/4 paydadaki ifade olacaktır, payı ise 2⁻²=1/4 alırsak, ifade şu şekilde yazılabilir.
(1/4).(4/(4m+1)=1/(4m+1) olacaktır.
1/(4m+1)=1/13
m=3 bulunur

Verilen ifadeleri açık şekilde yazarsak,
(2.2³/1000)+(64/1000)=80/1000=0,08 bulunur.

İlk ifadenin paydasını çarpanlarına ayırmamız yeterli olacaktır.
1+√a
(1+√a).(1-√a)
=
1
1-√a
şeklinde yazılır. Çıkarma işlemini yaparsak,
1-a
1-√a
=
5
3
(1+√a).(1-√a)
(1-√a)
=
5
3
(1+√a)=5/3
3+3√a=5
3√a=2
√a=2/3
a=4/9 bulunur.

İlk verilen işlemde B-B=0 olması gerekirken 9 verilmiş, öyleyse 10+D-C=4 yorumu yapılmalıdır. D-C=-6, C-D=6 olmalıdır.
Yine ilk işlemde A'dan B'ye bir yüzlük verildiğinden (A-1)-B=2, A-B=3 olmalıdır.
Yandaki işleme geçelim, 10A+C-10B-D=10(A-B)+C-D=36 bulunur.

a²-a=b²-b
a²-b²=a-b
(a-b).(a+b)=(a-b)
a+b=1 bulunur.
(a+b)²=1
(a+b)²=a²+2ab+b²=1
a²-2+b²=1
a²+b²=3 bulunur

2x=6x.6y-1
2x=2x.3x.6y-1
1=3x.6y-1
3x=1/6y-1
3x=61-y olacaktır.

x,y,z ye değer vermek kolayca sonuca ulaştırır.
x>0 olduğundan x=1 diyelim.
x+y<0 ise y=-2 diyelim.
y+z>x ise z=4 diyelim.
z>x>y doğru cevaptır.

a+b-1 ifadesini bulalım,
a+b=
x
x-y
+
y
x+y
=
x²+xy+xy-y²
x²-y²
a+b-1=
x²+xy+xy-y²
x²-y²
-
x²-y²
x²-y²
=
2xy
x²-y²
Payı bulmuş olduk, payda ise xy/(x²-y²) olacaktır.
Pay ve paydanın oranı ise 2 olarak bulunur.
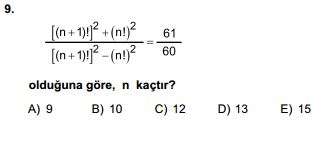
İfadeyi şu şekilde açalım,
(n+1)².n!²+n!²
(n+1)².n!²-n!²
=
61
60
n!²[(n+1)²+1]
n!²[(n+1)²-1]
=
(n+1)²+1
(n+1)²-1
=
61
60
=60.(n+1)²+60=61.(n+1)²-61
=(n+1)²=121
=n+1=11
=n=10 bulunur.

y-x=1 ise, x-y=-1
y-|-1|=2
y-1=2
y=3
yerine yazalım,
3-x=1
x=2
x+y=5 bulunur.

2x=3y=5z=90 olarak aldığımızda,
x=45
y=30
z=18
x+y+z=93, 100'e en yakın değer olacaktır.

13 parantezine alalım, 13(1+2+3+..+13)=13.14.13/2=13.13.7
Verilen ifadenin asal bölenleri 7 ve 13 olmak üzere 2 tanedir.

İlk sayı x olsun, sayıların toplamı;
x+x+2+x+4+x+6+x+8+x+10=6x+30 olacaktır.
4(x+10)=6x+30 verilmiş.
4x+40=6x+30
2x=10
x=5
En büyük sayı x+10=15 olur.

p=0
q=0
r=1 ifadelerin doğruluk değeridir.
0=>x ifadelerinin tamamı doğru olacağından, E şıkkındaki p=>(q^r) ifadesi de kesinlikle doğrudur.

b=1 için, 1-2-a-6-9
b=3 için 2-3-a-6-9
b=5 için sıralama yapılamıyor
b=8 için 3-6-a-8-9
b=10 için 3-6-a-9-10
Öyleyse cevap 5 olmalıdır.

d sayısı a ve b sayılarını tam bölmektedir.
I) a²/d²=(a/d)² olduğundan sonuç tam sayıdır.
II) (a²/d²)+b/d² olarak yazdığımızda, b/d² için kesin bir şey söylenemez.
III) (a²/d²)+(b²/d²) olarak yazdığımızda toplamdaki her iki ifade de tam sayı olduğundan sonuç tamsayıdır.
Cevap I ve III
Eline sağlık.
Hakkaten matematik soruları çok kolay sorulmuş bu yıl.(En azından bunlar.)
Hakkaten matematik soruları çok kolay sorulmuş bu yıl.(En azından bunlar.)

Aslında soruda bizden, 1, 2, 3, 4, 5, 6 rakamlarından 4 tanesini hepsini birer kez kullanarak toplayıp, en büyük ve en küçük toplamı elde etmemiz isteniyor.
1+2+3+4=10 en küçük
3+4+5+6=18 en büyük toplam,
18-10=8 aralarındaki farktır.

4*b ile b*4'ün sonucu aynı olmalı, işlem tablosunun sol tarafını kullanarak kontrol edelim,
b=1 için 4*1=5, 1*4=2, kümede bulunmaz,
b=2 için 4*2=4, 2*4=4, kümede bulunur.
b=3 için 4*3=1, 3*4=5, kümede bulunmaz
b=4 için 4*4=3, 4*4=3 kümede bulunur.
b=5 için 4*5=2, 5*4=2 kümede bulunur.
E) {2,4,5} bizden istenen cevaptır.

y=10 için x=75 en küçük değeridir, iki basamaklı olduğundan x=99 da en büyük değer olur.
Terim sayısı 99-75+1=25'tir.

Verilen tanıma göre
37+2=39=13.3 doğru
59+2=61 asal sayı olduğundan doğru
67+2=69=23.3 doğru
73+2=75=5.5.3 yanlıştır.
83+2=85=17.5 doğru

I)2(a+b)=2a.2b yanlış
II)2a+b=2a.2b doğru
III)(a+b)²=a².b² yanlış
Cevap yalnız II olmalıdır.

3 yılın ortalaması 4 milyon ise 3 yılda toplam 12 milyon kazanılmıştır.
4 yılda elde edilen ortalama kâr 4,5 milyon ise toplam 18 milyon kazanılmıştır.
Son yıl yani 2012'de 6 milyon kazanıldığı görülüyor.
Verilen bilgiye göre 2012 yılında kazanılan miktar, 2011 de kazanılanın 125/100 katıdır.
x.125/100=6
x.5/4=6
6x=24
x=4,8 bulunur.

Erkek fareler 12 saatte bir tablet alıyorsa günde 2 tablet alır.
Dişi fareler 8 saatte bir tablet alıyorsa günde 3 tablet alır.
Her erkek fare günde (0,5).2=1 gram ilaç alır.
Her dişi fare günde 1.3=3 gram ilaç alır.
Erkek sayısı x, dişi sayısı y olsun.
2x+3y=95 şeklinde bir denklem, tablet sayısından kurulur.
x+3y=85 denklemi ise ilaç miktarından kurulur.
Taraf tarafa çıkarırsak,
x=10 bulunur,
10+3y=85
3y=75
y=25
x+y=35 olacaktır.

Dağıtım günü sınıfta x öğrenci bulunsun.
36-3x kalem, 36-2x kalemtıraş, 36-x silgi artar.
108-6x=42 verilmiş,
6x=66
x=11 bulunur.
2x kalemtıraş dağıtıldığına göre, 22 kalemtıraş dağıtılmış, 14 kalemtıraş artmıştır.

Bir sonraki simetrik tarih 20.09.2009 dur.
Bunun için de 1 yıl 1 ay geçmelidir, yani 11 ay.
11.36=396 olacaktır cevabımız.

İsmi iki elemanlı işlemlerin içinde bulunanlar, işlemdeki diğer bilinmeyen elemanı da bulup üç elemanlı toplamı çözebileceğinden, bütün bilinmeyenlere ulaşabilirler.
Bu durumda isimleri iki elemanlı işlemlerde bulunan Ali Banu ve Doğa doğru cevaptır.

1-2-2, 1-3-1 veya 1-1-3 dağıtımları yapılabilir.
C(5,1).C(4,2).C(2,2)+C(5,1).C(4,3).C(1,1)+C(5,1).C(4,1).C(3,3)=30+20+20=70 olacaktır.

Çekilen toplar
10-5
9-6
8-7 olabilir, bunlardan yalnız biri 7 bulundurduğundan 1/3 cevabımız olur.

Attığımız boncukların toplamı şu şekilde artıyor,
1+2+3+4+5+...+n
Öyleyse en son n tane boncuk attığımızda toplam n.(n+1)/2 boncuk atılmış olur.
Bu toplamı bizden istenen 220. boncuğa yaklaştırmak için n=20 verelim.
20.21/2=210 tane boncuk atılmış olur.
En son 20 tane boncuk attık, bu 20 boncuk 5'in tam katı olduğundan 5. çubuğa atılmış olur.
Sıra şimdi 21 boncuğu 1. çubuğa atmaya geldi, 211'den 231'e kadar olan boncuklar 1. çubukta olacağından cevap A şıkkı 1 olacaktır.

Üçgenin bir kenarına 2x dersek, Çap 2√2.x olur, yarıçap ise √2.x olacaktır.
Yarıçapı √2.x olan çemberin çevresi 2∏r, yarım çemberin çevresi ∏r olacaktır, ∏=22/7, verilen yarım çemberin çevresi 22.√2.x/7 olacaktır.
Ayçanın yolu 4x, hızı 4 olduğundan süresi x olacaktır.
Barışın yolu 2√2.x, hızı 2 olduğundan süresi x√2 olacaktır.
Cemin yolu 22√2.x/7, hızı 3 olduğundan süresi (22/21).x√2 olacaktır.
Süreleri sıralandığında Ayça<Barış<Cem olduğundan yarış sıralaması
1. Ayça
2. Barış
3. Cem olacaktır.
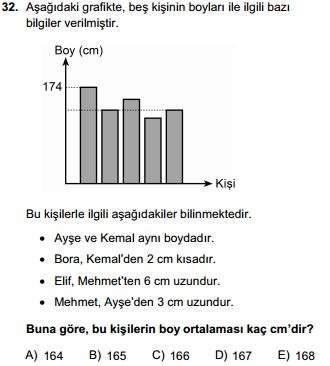
Ayşe ve Kemal aynı boyda ise 2. ve 5. sütunlar olmalıdır.
Bora Kemal'den 2cm kısa ise 4. sütun olmalıdır
Mehmet Ayşe'den 3cm uzun ise 3. sütun olmalıdır.
Elif Mehmet'ten 6cm uzun ise 1. sütun olmalıdır.
Elif 174 cm verilmiş,
Mehmet 168,
Ayşe ve Kemal 165
Bora 163 cm olarak bulunabilir.
(174+168+165+165+163)/5=167 olacaktır.
Eline sağlık.
Hakkaten matematik soruları çok kolay sorulmuş bu yıl.(En azından bunlar.)
Hakkaten matematik soruları çok kolay sorulmuş bu yıl.(En azından bunlar.)
eline sağlık Gökberk
Ben gittin sanmıştım. istersen tekrar moderatör ataması yapayım.
28.
Bu çözümde el altında bulunsun , değerler artsaydı tek tek saymayacaktık heralde.
O belli olan çocuğa bir tane verelim.(5 toptan birini seçip tabii ki)
Şimdi geriye 2 çocuk 4 farklı top kalacaktır.4 top 2 çocuğa 2^4 => 16 şekilde dağıtılabilir.Bunların içinden 1.0 , 0.1 durumlarını çıkaralım.16-2 => 14 durum olacaktır.
5.14 => 70 bulunur.
Bu çözümde el altında bulunsun , değerler artsaydı tek tek saymayacaktık heralde.
O belli olan çocuğa bir tane verelim.(5 toptan birini seçip tabii ki)
Şimdi geriye 2 çocuk 4 farklı top kalacaktır.4 top 2 çocuğa 2^4 => 16 şekilde dağıtılabilir.Bunların içinden 1.0 , 0.1 durumlarını çıkaralım.16-2 => 14 durum olacaktır.
5.14 => 70 bulunur.
