1-- x>0 olmak üzere,
x²-4≤0 eşitsizliğinin çözüm kümesi nedir? Cevap=(0,2]
Bu soruda x>0'ı -2 kökünü tabloya almayarak mı kullanıyoruz? Öyle de denedim ama 0 nereden geldi anlamadım çözüm kümesinde.
2--a<b<0<c olmak üzere,
<0 şartını sağlamayan x değerlerinin en geniş aralığı nedir? Cevap= [0,c]∪{a}
3--
<x-2 eşitsizliğini sağlayan x'in en küçük pozitif tam sayı değeri kaçtır? Cevap=5
4--x²-(m-2)x+9=0 denkleminin kökleri X1 ve X2dir.
0<X1<X2 olduğuna göre, m'nin değer alabileceği en geniş tanım aralığı nedir? Cevap= (8,∞)
5--x²-2x+m+2=0 denkleminin reel kökleri X1 ve X2dir.
X1<0<X2<5 şartını sağlayan en büyük m tam sayısı kaçtır? (-3)
x²-4≤0 eşitsizliğinin çözüm kümesi nedir? Cevap=(0,2]
Bu soruda x>0'ı -2 kökünü tabloya almayarak mı kullanıyoruz? Öyle de denedim ama 0 nereden geldi anlamadım çözüm kümesinde.
2--a<b<0<c olmak üzere,
(a-x)kare.(x-c)
bx
<0 şartını sağlamayan x değerlerinin en geniş aralığı nedir? Cevap= [0,c]∪{a}
3--
4
x+1
<x-2 eşitsizliğini sağlayan x'in en küçük pozitif tam sayı değeri kaçtır? Cevap=5
4--x²-(m-2)x+9=0 denkleminin kökleri X1 ve X2dir.
0<X1<X2 olduğuna göre, m'nin değer alabileceği en geniş tanım aralığı nedir? Cevap= (8,∞)
5--x²-2x+m+2=0 denkleminin reel kökleri X1 ve X2dir.
X1<0<X2<5 şartını sağlayan en büyük m tam sayısı kaçtır? (-3)
1)hayır, normal bir çözüm yapıyorsun sanki hiç x>0 ı vermemişler gibi sonra da x>0 (yani (0,∞)) ile bulduğun aralığın kesişimini alıyorsun ki eşitsizlikler sağlansın.
[-2,2]∩(0,∞)=(0,2]
2)
tablonun resmini koydum bu tabloya göre eşitsizliği sağlayan bölgeler (-∞,0)∪(c,∞)-{a} bunun dışında kalan bölge de sağlamaz dolayısıyla [0,c]∪{0}
[-2,2]∩(0,∞)=(0,2]
2)
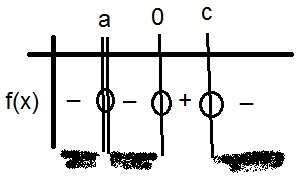
tablonun resmini koydum bu tabloya göre eşitsizliği sağlayan bölgeler (-∞,0)∪(c,∞)-{a} bunun dışında kalan bölge de sağlamaz dolayısıyla [0,c]∪{0}
1.soruda en son bölümde kesişim sonucunda açık kapalı aralığı nasıl ayarlıyoruz anlamadım. Yani neden [0-2) değil de (0,2] oldu onu anlamadım ya da -2 neden alınmadı?
Diğerini anladım teşekkür ederim.
Diğerini anladım teşekkür ederim.
kesişimde noktanın iki kümede de olması gerekir ama 0 ikinci kümenin elemanı değil o yüzden ( var ( " [ " yerine) 2 ise iki kümenin de elemanı o nedenle ] var ( " ) " yerine ) aradaki noktalar ise iki kümede de ortak olan elemanlar
Anladım şimdi çok teşekkür ederim.
