korkmazserkan 00:09 03 Ara 2014 #1 1)f(x)=arctanx olduğuna göre
Lim (f²(1+4h)-f²(1))/h=?
h-->0
2)g(x) ve k(x) fonksiyonları için
lim g(x)=6.dercede√5
x-->1
limk(x)=√2
x-->1
12.dereceden√17x+8≤f(x)≤g(x) ve k(x)≤h(x)≤√x+1
olduğuna göre
lim f(x).h(x) değeri nedir?
x-->1
Lim (f²(1+4h)-f²(1))/h=?
h-->0
2)g(x) ve k(x) fonksiyonları için
lim g(x)=6.dercede√5
x-->1
limk(x)=√2
x-->1
12.dereceden√17x+8≤f(x)≤g(x) ve k(x)≤h(x)≤√x+1
olduğuna göre
lim f(x).h(x) değeri nedir?
x-->1
∫
5
1
√-x²+6x-5dx
=?
2.soru cevabı 6√48 mi?
korkmazserkan 00:39 03 Ara 2014 #3 6√40 gösteriyor
2.soru
benim yanlış anlamam.
limg(x)=g(1)=6√5 gelir.
x-->1
limk(x)=k(1)=√2
x-->1
12√(17x+8)≤f(x)≤g(x) eşitsizliğinde x=1 için
12√25=6√5≤f(1)≤g(1)-ki g(1)=6√5 idi-
Buradan f(1)=6√5 gelir.
k(x)≤h(x)≤√(x+1) eşitsizliğinde x=1 için
k(1)≤h(1)≤√2 h(1)=√2=6√8 gelir.
limf(x).h(x)=f(1).h(1)=6√40
x-->1
Öteki sorular için konuya bakmam gerek. O yüzden onları yapamadım.
benim yanlış anlamam.
limg(x)=g(1)=6√5 gelir.
x-->1
limk(x)=k(1)=√2
x-->1
12√(17x+8)≤f(x)≤g(x) eşitsizliğinde x=1 için
12√25=6√5≤f(1)≤g(1)-ki g(1)=6√5 idi-
Buradan f(1)=6√5 gelir.
k(x)≤h(x)≤√(x+1) eşitsizliğinde x=1 için
k(1)≤h(1)≤√2 h(1)=√2=6√8 gelir.
limf(x).h(x)=f(1).h(1)=6√40
x-->1
Öteki sorular için konuya bakmam gerek. O yüzden onları yapamadım.
korkmazserkan 00:57 03 Ara 2014 #5
Eyvallah sağolasın teşekkürler
h=0 için;
L'hopital uygularsak;
h=0 için;
2.f(1).4.f'(1) olur.
f(x)=arctanx olarak verilmiş.
f²(1)-f²(1)
0
=
0
0
L'hopital uygularsak;
lim
h→0
2.f(1+4h).4.f'(1+4h)
1
h=0 için;
2.f(1).4.f'(1) olur.
f(x)=arctanx olarak verilmiş.
f(1)=arctan1=
∏
4
f'(x)=
1
1+x²
f'(1)=
1
1+1²
=
1
2
2.f(1).4.f'(1)=
2.∏
4
.
4.1
2
=∏
korkmazserkan 01:04 03 Ara 2014 #7
sağol nymphe görememişim teşekkürler
Süleyman Oymak 02:48 03 Ara 2014 #8 
korkmazserkan 16:13 03 Ara 2014 #9
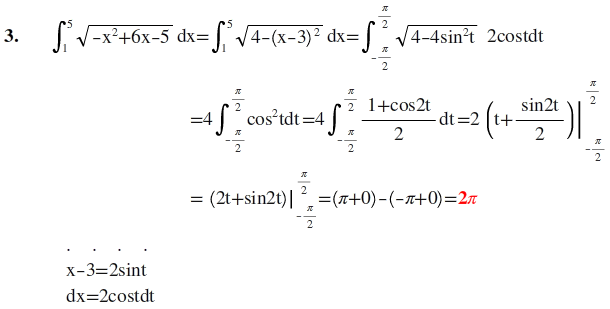
Teşekkürler hocam açıklayıcı olmuş