Bölme-2

Çözen arkadaşlara şimdiden teşekürler

Sayın üye lütfen sorunuzu forum kurallarına uygun biçimde yazınız.

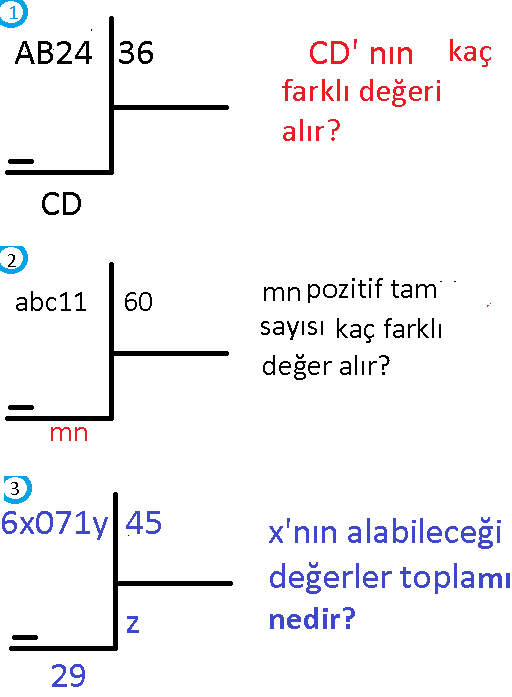
1) AB24/36K+CD CDnın kaç farklı değerli vardır?
2)abc11/60k+mn mn pozitif tam sayısı kaç farklı değer alır?
3)6x071y/45z+29 x'nın alabileceği değerler toplamı kaçtır?

Böyle pek anlaşılır olmadıgı için paitte çizdim.

Çözen yokmu arkadaşlar?

1.
100AB+24=36k+CD verilmiş
100,24 ve 36 4 ile bölünebildiğinden CD de bölünmelidir. CD=4N olsa
25AB+6=9k+N olur , AB üzerinde bir kısıtlama olmadığından ve 25 ile 9 aralarında asal olduğundan 25AB sayısı 9 modunda istenilen değere eşitlenebilir böylece 25AB+6 sayısı de tüm kalanlar sınıfını taramış olur. yani N=0,1,2,3,...,8 yapılabilir , tek kısıt CD nin 2 basamaklı olması ki bu da N>2 olmasını gerektirir böylece 9-3=6 farklı değer alır.

2.
ilk soruya benzer şekilde abc üzerinde bir kısıtlama olmadığından ve obeb(100,60)=20 olduğundan 60/20=3 farklı değer oluşur. bunlar 11,31,51 olur ve hepsi de 2 basamaklıdır yani cevap 3 oluyor.

3.
6x071y=45.z+29 verilmiş
45 e yani 5 ve 9 a göre inceleme yapılması lazım.
6x071y=4 (mod5) → y=4 veya 9 , 6x071y=2 (mod9) → x+y=6 (mod9) → x+y=6 veya x+y=15

y=4 olduğunda x+y=6 → x=2 , x+y=15 için x çözümü gelmez
y=9 olduğunda x+y=6 için çözüm oluşmaz , x+y=15 için de x=6 çözümü elde edilir.
2 farklı x değeri bulunmuş olur, toplamları da 2+6=8 bulunur.

Çok teşekürler.

usta bu kısmı anlayamadım ya, burada ne demek istedin?

bir de ikinci soruda neden 100 ile 60'ın obebini aldık? 60/20 ye nasıl ulaştık?

burada 25AB sayısının AB nin değeri değiştirilerek 9 modunda istenilen değeri alabileceği söylenmiş.
yani 25.AB=x (mod9) denkliğinde her x için AB bulunabileceğini söylüyoruz. bunu sağlatan şey 25 ile 9 un aralarında asal olması , 25 ile 9 aralarında asal olmasa mesela obebleri d gibi bir sayı olsa x in de d ye bölünmesi gerekeceğinden x sadece d,2d,3d,4d,... değerlerini alabilirdi. yine uzatıyorum mesela 25.AB değil de elimizde 24.AB gibi bir ifade olsaydı x=0,3,6 değerlerini alabilir derdik çünkü obeb(24,9)=3

ikinci sorunuz da böylece açıklanmış oluyor. elde ettiğimiz iki sayının obebi 20 olduğundan ve kalan 11 olduğundan kalan değerleri genel halde 20k+11 şeklinde olabilir. kalan 60 dan büyük olamayacağından 60/20=3 tane değer alabilir bunlar da 11,11+20=31,11+40=51
hepsi de istenen özelliğe sahip olduğundan eleme yapmamıza gerek yok.(ilk soruda 0,1,2 değerlerini elemiştik çünkü iki basamaklı sonuç oluşturamıyorlardı)

teşekkür ederim.
mesela şu soruda;
ABC48=60k+EF (ABC48 5 basamaklı bir sayı, EF iki basamaklı bir sayı)
100ABC+48=60K+EF
100,48,60 4 ün katı o yüzden EF de dördün katı olmalıdır
EF=4N dersek
25ABC+12=15K+N şekline getirdim.
25ABC+12=N (mod15) şeklinde yazdıktan sonra takıldım..