Nasılyaniya 17:57 22 Eyl 2014 #1 1)
2)
3)
4)
lim
x→∏/8
sin5x.sin2x
cos3x−cos7x
değeri kaçtır? 1/2
2)
lim
x→1
x³−mx²+n
x−1
=−1 ise m+n? 3
3)
lim
x→0
3x−tan2x
2x+sin3x
limitinin değeri kaçtır? 1/5
4)
lim
x→0⁺
sinx
√1−cosx
değeri kaçtır? √2
Nasılyaniya 13:44 23 Eyl 2014 #2 yukarı
1.soru
Bu soruyu cosx-cosy=-2.sin1/2(x+y).sin1/2(x-y) formülünden yapacaksın.
cos3x-cos7x=-2.sin1/2(3x+7x).sin1/2(3x-7x)
cos3x-cos7x=-2sin5x.sin(-2x)
daha sonra sin(-x)=-sinx şeklinde yazılır. yukarıdaki ifadeyi düzenle
-2sin5x.(-sin2x)=2sin5x.sin2x bunu yerine yazarsan sadeleşmelerden 1/2 gelir.
Bu soruyu cosx-cosy=-2.sin1/2(x+y).sin1/2(x-y) formülünden yapacaksın.
cos3x-cos7x=-2.sin1/2(3x+7x).sin1/2(3x-7x)
cos3x-cos7x=-2sin5x.sin(-2x)
daha sonra sin(-x)=-sinx şeklinde yazılır. yukarıdaki ifadeyi düzenle
-2sin5x.(-sin2x)=2sin5x.sin2x bunu yerine yazarsan sadeleşmelerden 1/2 gelir.
2.soru
x=1 için 1/0 ifadesi geliyor. yani tanımsız. Buradan l'hospital yapılacak. limit'te bu tür belirsizliklerde l'hospital kuralı uygulanır. Yani pay ve paydanın ayrı ayrı türevleri alınır.
(x³-mx²+n)'=3x²-2mx
(x-1)'=1 bunları yerine yaz
lim(3x²-2mx)/1=-1
x=1
x=1 için 3-2m/1=-2
buradan m=2 gelir.
En başta limit 1/0 gelmişti.Ama limitin bir sonucu var.
Buradan şu anlaşılıyor. x³-mx²+n'nin içinde x-1 çarpanı var. yani x=1 için bu ifade de sıfır olmalı.
x=1 için
1³-m.1²+n=0
n-m=-1 gelir. m=2 için
n=1 gelir.
m+n=3 gelir.
x=1 için 1/0 ifadesi geliyor. yani tanımsız. Buradan l'hospital yapılacak. limit'te bu tür belirsizliklerde l'hospital kuralı uygulanır. Yani pay ve paydanın ayrı ayrı türevleri alınır.
(x³-mx²+n)'=3x²-2mx
(x-1)'=1 bunları yerine yaz
lim(3x²-2mx)/1=-1
x=1
x=1 için 3-2m/1=-2
buradan m=2 gelir.
En başta limit 1/0 gelmişti.Ama limitin bir sonucu var.
Buradan şu anlaşılıyor. x³-mx²+n'nin içinde x-1 çarpanı var. yani x=1 için bu ifade de sıfır olmalı.
x=1 için
1³-m.1²+n=0
n-m=-1 gelir. m=2 için
n=1 gelir.
m+n=3 gelir.
Nasılyaniya 17:53 23 Eyl 2014 #5
Teşekkür ederim 
4.soru
(sinx)/[√(1-cosx)] bu ifadeyi √(1+cosx) ile genişlet. ifade
sinx.√(1+cosx)/√(1-cos²x) gelir.
1-cos²x=sin²x'tir. yerine yaz.
sinx.√(1+cosx)/√sin²x)=√1+cosx gelir. x=0 için √2 değeri gelir.
(sinx)/[√(1-cosx)] bu ifadeyi √(1+cosx) ile genişlet. ifade
sinx.√(1+cosx)/√(1-cos²x) gelir.
1-cos²x=sin²x'tir. yerine yaz.
sinx.√(1+cosx)/√sin²x)=√1+cosx gelir. x=0 için √2 değeri gelir.
3.soru
Bu soruda aklıma gelen tek yol l'hospital. x, sıfıra giderken pay ve payda 0 oluyor.
(3x-tan2x)'=3-2.sec²2x
(2x+sin3x)'=2+3cos3x
x=0 için
pay=3-2=1
payda=2+3=5 gelir.
Bu soruda aklıma gelen tek yol l'hospital. x, sıfıra giderken pay ve payda 0 oluyor.
(3x-tan2x)'=3-2.sec²2x
(2x+sin3x)'=2+3cos3x
x=0 için
pay=3-2=1
payda=2+3=5 gelir.
VEYA
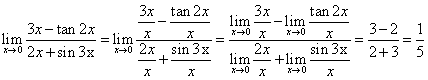
Diğer çözümlü sorular alttadır.