1)En az 3 tane ortak pozitif böleni bulunan birbirinden farklı üç tane 2 basamaklı doğal sayının toplamı en az kaçtır?48
2)Boyutları 16x18x22 cm³ olan dikdörtgenler prizması biçimindeki bir cismin bir köşesinden 1000 cm³ olan küp biçimindeki parçası çıkarılıyor.
Bu cismin geriye kalan kısmı birbirine eş ,küp biçiminde en az kaç parçaya bölünebilir?667
3)Ondalık yazılımında sıfırdan farklı tüm rakamlarına bölünebilen sayıya ŞAHİN sayı diyelim
Buna göre en fazla kaç tane pozitif ardışık ŞAHİN SAYI vardır? 12
4)41,70 ve 215 sayılarının her birinin a ile bölümünden elde edilen kalanlar aynı ve b dir
a>1 ise a-b farkı kaçtır? 17
5)Bir havuzu A musluğu tek başına 15 saatte doldururken B musluğu 21 saatte boşaltmaktadır
Havuz boş iken A musluğu açıldıktan kaç dakika sonra B musluğu açılırsa havuzun yarısı 10 saatte dolar? 390
2)Boyutları 16x18x22 cm³ olan dikdörtgenler prizması biçimindeki bir cismin bir köşesinden 1000 cm³ olan küp biçimindeki parçası çıkarılıyor.
Bu cismin geriye kalan kısmı birbirine eş ,küp biçiminde en az kaç parçaya bölünebilir?667
3)Ondalık yazılımında sıfırdan farklı tüm rakamlarına bölünebilen sayıya ŞAHİN sayı diyelim
Buna göre en fazla kaç tane pozitif ardışık ŞAHİN SAYI vardır? 12
4)41,70 ve 215 sayılarının her birinin a ile bölümünden elde edilen kalanlar aynı ve b dir
a>1 ise a-b farkı kaçtır? 17
5)Bir havuzu A musluğu tek başına 15 saatte doldururken B musluğu 21 saatte boşaltmaktadır
Havuz boş iken A musluğu açıldıktan kaç dakika sonra B musluğu açılırsa havuzun yarısı 10 saatte dolar? 390
1)En az 3 tane ortak pozitif böleni bulunan birbirinden farklı üç tane 2 basamaklı doğal sayının toplamı en az kaçtır?48
Bunu anlatmak benim için güç olacak ama çıtlatayım, anlarsın umarım.
Şimdi biliyorsun 1 sayısı bütün doğal sayıları böler. Bize lazım olan diğer iki pozitif bölen. Şimdi en az dediği için 2 sayısını da koyduk cebe. Yani bu iki basamaklı sayıların içinde muhakkak 1 ve 2 çarpanları yani 2 çarpanı olmak zorunda.
Gelelim üçüncü çarpana. Akla direkt 3 gelir, bu sefer iki basamaklı sayıların içinde 1 , 2 ve 3 çarpanı olmak zorunda, yani 6 çarpanı olmak zorunda olacak ama şöyle bir şey var. Eğer bir tane daha iki çarpanı olsa??
İki tane 2 çarpanı olsa 1 tane 1, 2 tane 2 çarpanı yani iki basamaklı sayılarda 4 çarpanı olmak zorunda olacak. Bu sayıların pozitif bölenleri 1,2 ve 4 olacaktır.
O halde dördün katı olan en küçük iki basamaklı doğal sayıyı bulup yanına iki tane daha eklemeli;
12+16+20=48
Bunu anlatmak benim için güç olacak ama çıtlatayım, anlarsın umarım.
Şimdi biliyorsun 1 sayısı bütün doğal sayıları böler. Bize lazım olan diğer iki pozitif bölen. Şimdi en az dediği için 2 sayısını da koyduk cebe. Yani bu iki basamaklı sayıların içinde muhakkak 1 ve 2 çarpanları yani 2 çarpanı olmak zorunda.
Gelelim üçüncü çarpana. Akla direkt 3 gelir, bu sefer iki basamaklı sayıların içinde 1 , 2 ve 3 çarpanı olmak zorunda, yani 6 çarpanı olmak zorunda olacak ama şöyle bir şey var. Eğer bir tane daha iki çarpanı olsa??
İki tane 2 çarpanı olsa 1 tane 1, 2 tane 2 çarpanı yani iki basamaklı sayılarda 4 çarpanı olmak zorunda olacak. Bu sayıların pozitif bölenleri 1,2 ve 4 olacaktır.
O halde dördün katı olan en küçük iki basamaklı doğal sayıyı bulup yanına iki tane daha eklemeli;
12+16+20=48
2. Soru:
Ayrıtları şöyle olan bir cisim olsun

OBEB(16,18,22)=2
Yani 16'lık kısımdan 8,
18'lik kısımdan 9,
22'lik kısımdan 11 parça ayırabiliriz.
8.9.11=792 tane küp yapılır.
Hacmi 1000cm3 olan küp çıkarılıyormuş. Bütündeki parça sayısını hesaplarken 2 üzerinden gitmiştik, şimdi yine aynı şekilde 10-10-10 ayrıtı olan bu kısma kaç küp düşüyor ona bakarsak 5.5.5=125 tane küp düşer.
792-125=667 olur.
Ayrıtları şöyle olan bir cisim olsun
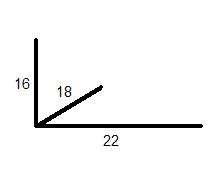
OBEB(16,18,22)=2
Yani 16'lık kısımdan 8,
18'lik kısımdan 9,
22'lik kısımdan 11 parça ayırabiliriz.
8.9.11=792 tane küp yapılır.
Hacmi 1000cm3 olan küp çıkarılıyormuş. Bütündeki parça sayısını hesaplarken 2 üzerinden gitmiştik, şimdi yine aynı şekilde 10-10-10 ayrıtı olan bu kısma kaç küp düşüyor ona bakarsak 5.5.5=125 tane küp düşer.
792-125=667 olur.
4. Soru:
41=a.x+b
70=a.y+b
215=a.z+b
şeklinde yazdığımızda herhangi ikisinden b'yi çekip eşitleyelim.
41-a.x=70-a.y
29=a(y-x) burda 29 asal sayı olduğuna göre a=1 veya a=29 olacaktır ancak a>1 şartı olduğundan a=29 alırız.
41'i 29'a böldüğümüzde de b'yi 12 buluruz.
29-12=17 olur.
41=a.x+b
70=a.y+b
215=a.z+b
şeklinde yazdığımızda herhangi ikisinden b'yi çekip eşitleyelim.
41-a.x=70-a.y
29=a(y-x) burda 29 asal sayı olduğuna göre a=1 veya a=29 olacaktır ancak a>1 şartı olduğundan a=29 alırız.
41'i 29'a böldüğümüzde de b'yi 12 buluruz.
29-12=17 olur.
A tek basina 15 saat b tek basina 21 saat
Havuz 15.21.2=630 lt olsun
Muslugu saatte 630/15=42 lt dolduru b muslugu 630/21= 30 lt satte bosaltir
Havuzun yarini 315 lt olur
42.x+(42-30)(10-x)=315 denklemi yaparsak x=195/30 saat gelir .60 = 390 dakika
kusura bakmauin telefondan anlattik biraz karisik oldu
Havuz 15.21.2=630 lt olsun
Muslugu saatte 630/15=42 lt dolduru b muslugu 630/21= 30 lt satte bosaltir
Havuzun yarini 315 lt olur
42.x+(42-30)(10-x)=315 denklemi yaparsak x=195/30 saat gelir .60 = 390 dakika
kusura bakmauin telefondan anlattik biraz karisik oldu
herkese teşekkürler üçünü soru günceldir
3.
şu an zamanım kısıtlı ancak yanıt 13.
Eski yıllardan bir Tübitak 1.aşama sınav sorusunun benzeri.hatta aynısı orada şahin yerine özel sayı diyor ancak bu çözümü değiştirmiyor elbette
şu an zamanım kısıtlı ancak yanıt 13.
Eski yıllardan bir Tübitak 1.aşama sınav sorusunun benzeri.hatta aynısı orada şahin yerine özel sayı diyor ancak bu çözümü değiştirmiyor elbette
herkese teşekkürler üçünü soru günceldir
bu şekildeki en uzun ardışık dizinin uzunluğu 10 dan az olmasın.
dizide son rakamı atıyorum 4 ve 5 olan ardışık iki terime bakarsak, bu iki sayının birden son rakam hariç tüm rakamlara bölünmesi gerekir ki bu bölenlerin sonu 4 ve 5 olan bu iki sayının obebi olan 1 de bölmeleri gerekir yani 1 olmaları (ya da 0).
kısaca son basamak hariç tüm basamakların ya 0 ya da 1 olması gerekir.
ayrıca bu sayıların arasındaki fark 10 olacağından sonu 3,4,6,7,8,9 olan iki tane sayı bulunamaz.
kısaca en uzun son iki basamak listesi
00,01,02,...,09,10,11,12 olacak şekilde 13 sayı olarak bulunur.
şimdi bunun bulunabileceğini de göstermek lazım (12 bulunabiliyor , 1 den 12 ye kadar pozitif sayılar)
X00 şeklinde, 3 ve 7 sayılarına (ikincil olarak da 9 a) bölünebilen ve x in sadece 1 ve 0 lardan oluştuğu bir sayı arıyoruz. fazla uzatmayalım çin kalan teoremine göre böyle bir sayı vardır.
sonucu olarak bu x00 sayısıyla başlayan 13 sayı en uzun dizilerden birisi olarak bulunmuş olur.
