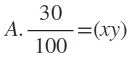1) A= (abababab)x/(ab)x
ifadesi veriliyor.
Buna gore A nin x^2-x+1 ile bolumunden kalan kactir?(1)
2) 12^3 - 8^3 sayisi 4 tabaninda yazilirsa kac basamakli bir sayi elde edilmis olur?(6)
3)On basamakli 999...9 sayisi 283 ile carpiliyor
Elde edilen sayini rakamlari toplami kactir?(90(
4)Hazal sahip oldugu 150 boncugu farkli sayilarda olmak kosuluyla arkafaslarina dagitiyor.Hazalin boncuk verdigi arkadaslarinin sayisi en cok kac olabilir?(16(
5)Pozitif bir A tam sayisinin %30 u iki basamakli bir sayidir.Buna gore A kac farkli deger alir?(30)