Taban Aritmetiği

Soru:1
8 sayı tabanı ve k ile m doğal sayılardır.
(543212345)₈=8.k+m eşitliğini sağlayan en küçük m değeri kaçtır?(ÇÖZÜLDÜ)
Soru:2

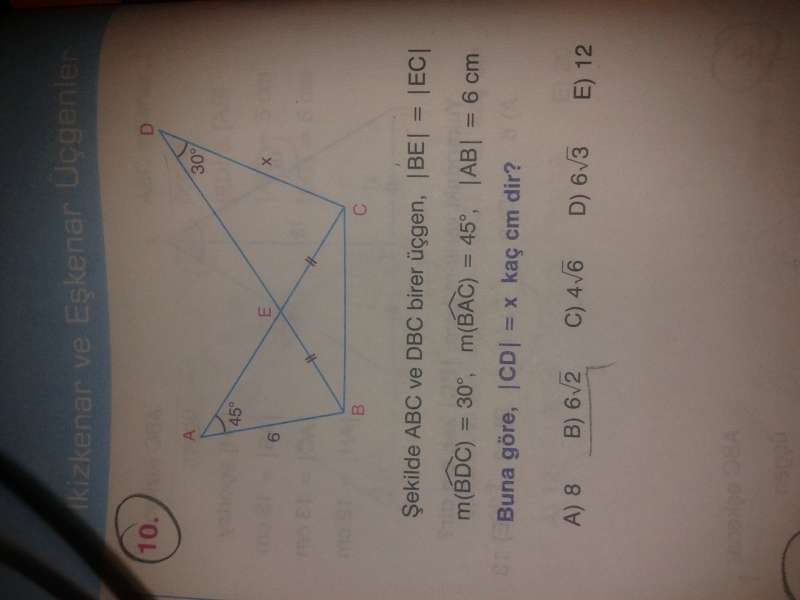
Soru:3

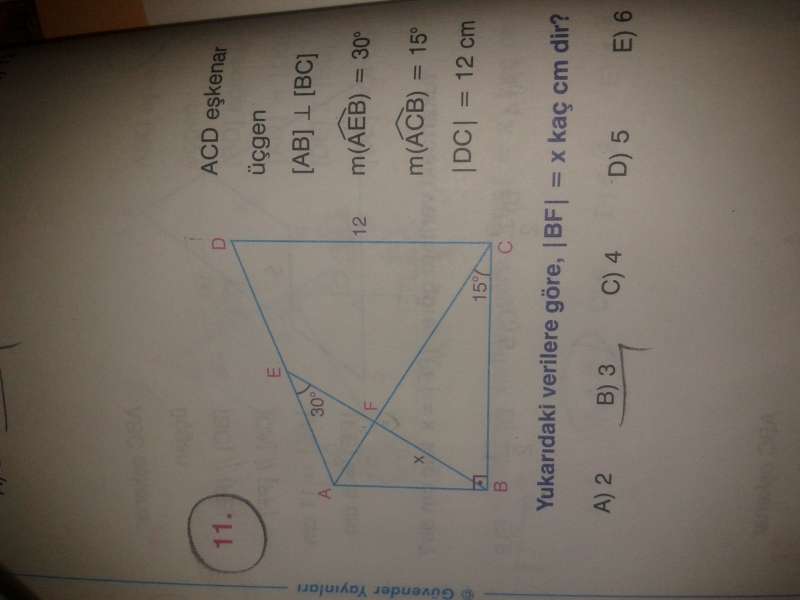
Soru:4

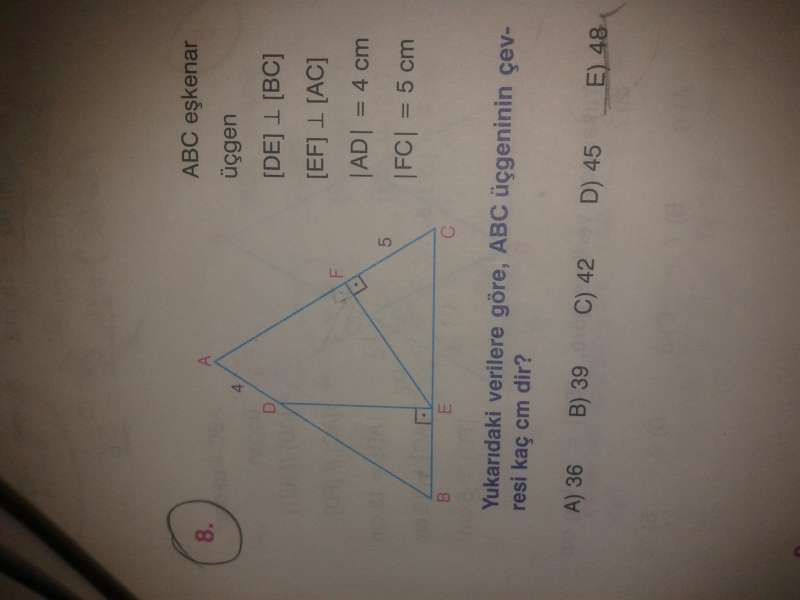
Soru:5

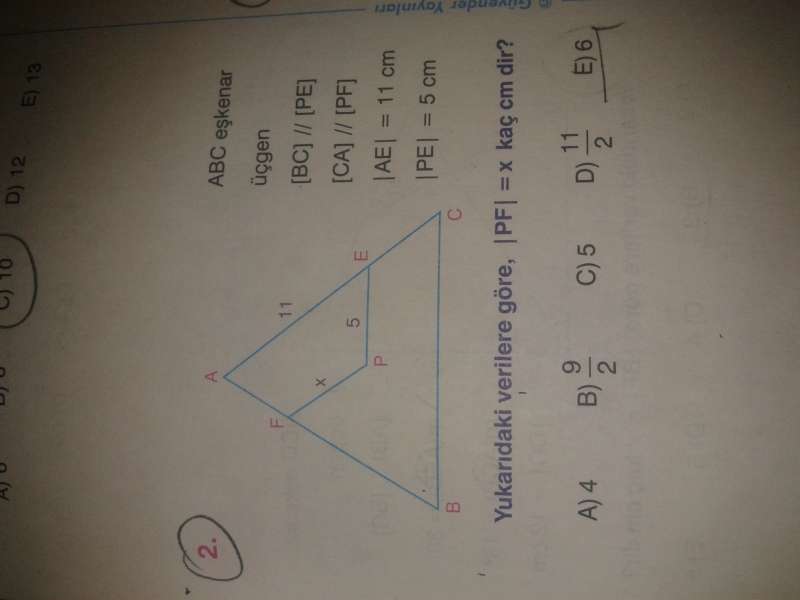
1)
Yani bu sayının 8'e bölümünden kalan isteniyor.
Sayı da zaten 8 tabanında olduğu için 8'e bölümünden kalan birler basamağı yani 5'dir.

Anlamadım biraz daha açabilir misin?

Sayıyı çözümlersek
5.8⁰+4.8¹+3.8²+...
Kırmızı yer zaten 8'e bölündüğünden bu sayının 8'e bölümünden kalan 5.8⁰=5 olur.
Zaten soru da en küçük m değeri diyerek 8'e bölümünden kalanı sormuş.
10 tabanındaki sayıların 10'a bölümünden kalanı bulmak için birler basamağını buluyoruz ya onun gibi.

Teşekkürler şimdi anladım

Yeni sorular eklendi.

2)
B'den AC'ye dik çekelim dik'in uzunluğu 45-45-90 üçgeninden 3√2 olur.
Aynı şekilde C'den BD'ye dik çekersek yine 3√2 olur (eş üçgenler)
Dolayısıyla x=6√2 (30-60-90 üçgeni )

3)
DAC açısı 60 derece olduğundan BFA 90 derecedir.
Eşkenar üçgenden AC=12 ve 15-75-90 üçgeninde yükseklik hipotenüsün dörtte biri olduğundan |BF|=3

4)
30-60-90 üçgeninden |EC|=10 olur.
|BE|=x dersek yine 30-60-90 üçgeninden |BD|=2x
2x+4=x+10
x=6 bulunur öyleyse eşkenar üçgenin bir kenarı 16'dır ve çevresi 48'dir.

5)
EP'yi uzatalım AB'ye D'de dokunursa FPD eşkenar olduğundan PD=x bulunur.
Aynı zamanda AED de eşkenar üçgen olduğundan x+5=11 yani x=6