1) d noktasından bc ye bir dikme inelim ve dikme ayağı e noktası olsun. |de|=3 olacağı açıktır.
(|ad|=|dc|=|hc| olduğuna dikkat ediniz)
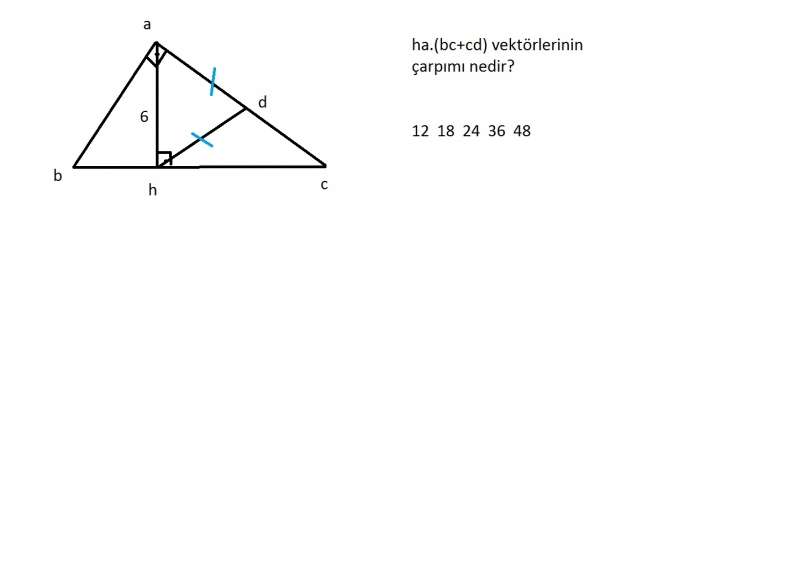
ha.(bc+cd)=ha.(bc+ce+ed)=ha.bc+ha.ce+ha.ed
ha ile bc dik olduğuna göre ha.bc=0,
ha ile ce dik olduğuna göre ha.ce=0,
ha ile ed paralel (hatta aynı yönlü) olduğuna göre ha.ed=|ha|.|ed|=6.3=18
2) çözümünüz doğru. cevap olarak paralel iki doğru yerine dik iki doğru olmalı. (bunun literatürdeki adı "dejenere hiperbol" dür.)
3) y²=16x parabölünün doğrultman doğrusu x=-4 tür. x²=24y parabolünün doğrultman vektörü y=-6 dır. Bu iki doğrusunun eksenlerler sınırladığı bölde kenar uzunlukları 4 ve 6
br olan dikdörtgendir ve bunun çevresi 20
br dir.
4) Bir (x,y) noktasının F(4,0) noktasına olan uzaklığı √
(x-4)²+y² dir. Aynı noktanın x=-4 doğrusuna uzaklığı |x+4| tür. Bu iki uzaklık eşit ise (x-4)²+y²=(x+4)² ve buradan y²=16x bulunur.
NOT: Aslında burada istenen odak noktası F(4,0) ve doğrultman doğrusu x=-4 olan parabolün denklemidir. 5) x+2y+4=0 doğrusuna dik doğru denklemi y=2x+b şeklindedir. Bu doğru hiperböle teğet ise hiperböl denkleminde y yerine 2x+b yazınca elde edeceğimiz x türünden ikinci dereceden denklemin diskriminantı 0 olmalıdır.
Bunu yapınca b=2√
5 veya b=-2√
5 bulunur.