1
x²+y²-(k+4)x+(k-4)y=0 çemberinin merkezi x ekseni üzerindeyse r=? (4)
2
x-y-4=0 doğrusuna paralel olan birim vektör hangisidir? (1/√2, 1/√2)
3
x²+4y²=8 elipsine üzerindeki (2,-1) noktasından çizilen teğetin denklemi nedir? (x-2y-8=0)
4
(x²/8)+(y²/b²)=1 elipsi ile y=-x+4 doğrusu teğetse yedek eksen uzunluğu kaç birimdir? (4√2)
5
2x²+3y²=12 elipsinin y=4x-2 doğrusuna paralel teğetlerinin denklemleri nedir?
6
x²+2y²=2 elipsine K(0,3) noktasından çizilen teğetlerden birinin denklemi nedir? (y=2√2x+3)
7
merkezil elipsin asal eksen uzunluğu 4√3 birim ve yedek eksen uzunluğu 2 birimdir. Elipsin y=-2x dorusuna paralel teğetlerinden birinin x eksenini kestiği noktanın apsisi kaç olabilir? (7/2)
8
(x²/8)+(y²/2)=1 elipsi ile y=2x+n doğrusu teğetse n hangisi olabilir? (√34)
(y değerini elips denkleminde yerine yazdığımızda n ye ulaşabiliyoruz. Bu soruyu türevle nasıl çözeriz, onu merak ettim. 3. bir yol da var mıdır?)
x²+y²-(k+4)x+(k-4)y=0 çemberinin merkezi x ekseni üzerindeyse r=? (4)
2
x-y-4=0 doğrusuna paralel olan birim vektör hangisidir? (1/√2, 1/√2)
3
x²+4y²=8 elipsine üzerindeki (2,-1) noktasından çizilen teğetin denklemi nedir? (x-2y-8=0)
4
(x²/8)+(y²/b²)=1 elipsi ile y=-x+4 doğrusu teğetse yedek eksen uzunluğu kaç birimdir? (4√2)
5
2x²+3y²=12 elipsinin y=4x-2 doğrusuna paralel teğetlerinin denklemleri nedir?
6
x²+2y²=2 elipsine K(0,3) noktasından çizilen teğetlerden birinin denklemi nedir? (y=2√2x+3)
7
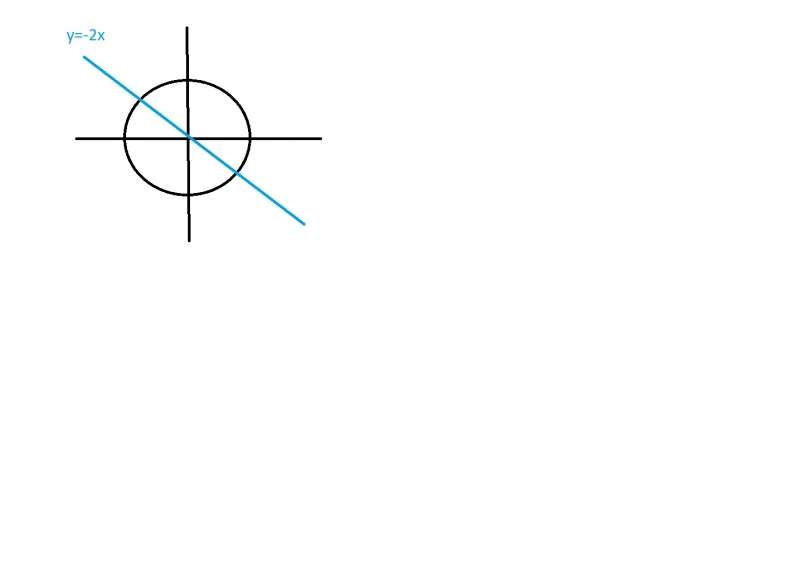
merkezil elipsin asal eksen uzunluğu 4√3 birim ve yedek eksen uzunluğu 2 birimdir. Elipsin y=-2x dorusuna paralel teğetlerinden birinin x eksenini kestiği noktanın apsisi kaç olabilir? (7/2)
8
(x²/8)+(y²/2)=1 elipsi ile y=2x+n doğrusu teğetse n hangisi olabilir? (√34)
(y değerini elips denkleminde yerine yazdığımızda n ye ulaşabiliyoruz. Bu soruyu türevle nasıl çözeriz, onu merak ettim. 3. bir yol da var mıdır?)
mathematics21 14:59 04 May 2013 #2 1) Merkezi (a,b) yarıçapı r olan çemberin denklemi
(x-a)²+(y-b)²=r² yani x²+y²-2ax-2by+a²+b²-r²=0 olduğunu biliyoruz.
Merkezi x ekseni üzerinde olan çember için merkez M(a, 0) şeklinde bir noktadır. Yani b=0 olmalıdır. Bu durumda çember denkleminde y² dışında y li terim olmamalıdır.
Verilen denkleme göre merkez x ekseni üzerinde ise k=4 olmalıdır.
Bu durumda çember denklemi x²+y²+8x=0 olur. Tam kareye tamamlayarak
x²+8x+16+y²=16
(x+4)²+y²=16 elde edilir.
M(-4, 0) ve r=4 tür.
(x-a)²+(y-b)²=r² yani x²+y²-2ax-2by+a²+b²-r²=0 olduğunu biliyoruz.
Merkezi x ekseni üzerinde olan çember için merkez M(a, 0) şeklinde bir noktadır. Yani b=0 olmalıdır. Bu durumda çember denkleminde y² dışında y li terim olmamalıdır.
Verilen denkleme göre merkez x ekseni üzerinde ise k=4 olmalıdır.
Bu durumda çember denklemi x²+y²+8x=0 olur. Tam kareye tamamlayarak
x²+8x+16+y²=16
(x+4)²+y²=16 elde edilir.
M(-4, 0) ve r=4 tür.
mathematics21 15:06 04 May 2013 #3 2) ax+by+c=0 doğrusu v=(a, b) vektörüne diktir. v vektörüne dik olan vektörler doğruya paralel olacaktır. u=(-b, a) veya u=(b, -a) vektörleri v ye dik olduğuna göre bu vektörler ve bu vektörlerin sıfırdan farklı her katı ax+by+c=0 doğrusuna paraleldir. Aslında bu iki vektör de biribirinin -1 katıdır.
x-y-4=0 doğrusuna dik olan vektör v=(1, -1) yönündedir. Bu doğruya paralel olan vektör u=(1,1) veya bunun herhangi bir katıdır. Aradığımız birim vektör için bu vektörü kendi boyuna bölmeliyiz. |u|=√2 olduğuna göre
(1/√2, 1/√2) vektörü verilen doğruya paralel bir birim vektördür.
NOT: (-1/√2, -1/√2) vektörü de verilen doğruya paralel bir birim vektördür.
x-y-4=0 doğrusuna dik olan vektör v=(1, -1) yönündedir. Bu doğruya paralel olan vektör u=(1,1) veya bunun herhangi bir katıdır. Aradığımız birim vektör için bu vektörü kendi boyuna bölmeliyiz. |u|=√2 olduğuna göre
(1/√2, 1/√2) vektörü verilen doğruya paralel bir birim vektördür.
NOT: (-1/√2, -1/√2) vektörü de verilen doğruya paralel bir birim vektördür.
mathematics21 15:17 04 May 2013 #4 3) Verilen elips denkleminin x'e göre tüverini alalım. (Tabii y=y(x) şeklinde bir fonksiyon olarak kabul ederek)
2x+8y.y'=0
x=2, y=-1 için y' ifadesi aradığımızı teğetin eğimidir.
2.2+8.(-1).m=0 buradan m=1/2 bulunur.
Eğimi 1/2 olan ve (2,-1) noktasından geçen doğru denklemi y+1=1/2(x-2) dir. Bu da x-2y-4=0 şeklinde yazılabilir. (Cevabınızı kontrol edin lütfen)
NOT: Birçok kaynak elips veya çember için bu tür teğet denklemlerine formül verirler. Asla o formülleri ezberlemenizi tavsiye etmiyorum. Şu an için türev görmemiş olsanız bile ileride göreceksiniz. Zaten o kitaplarda verilen formüller de türevin uygulamalarından çıkan sonuçlardır.
2x+8y.y'=0
x=2, y=-1 için y' ifadesi aradığımızı teğetin eğimidir.
2.2+8.(-1).m=0 buradan m=1/2 bulunur.
Eğimi 1/2 olan ve (2,-1) noktasından geçen doğru denklemi y+1=1/2(x-2) dir. Bu da x-2y-4=0 şeklinde yazılabilir. (Cevabınızı kontrol edin lütfen)
NOT: Birçok kaynak elips veya çember için bu tür teğet denklemlerine formül verirler. Asla o formülleri ezberlemenizi tavsiye etmiyorum. Şu an için türev görmemiş olsanız bile ileride göreceksiniz. Zaten o kitaplarda verilen formüller de türevin uygulamalarından çıkan sonuçlardır.
mathematics21 15:30 04 May 2013 #5 4)
Teğetin değme noktası (a, 4-a) olsun. Bu nokta elips üzerinde olduğuna göre elipsin denklemini sağlar.
a²/8+(4-a)²/b²=1 olmaldır. ...(I)
Verilen elips denkleminin x'e göre türevini alalım: 2x/8+2y.y'/b²=0
(a, 4-a) noktasında çizilen teğetin eğimi m=-1 olduğuna göre son denklemde x=a, y=4-a ve y'=-1 olmalıdır. Buradan
a/8+(a-4)/b²=0 ... (II) elde edilir.
(II) ifadesinden b²=8(4-a)/a bulunur. Bunu (I) ifadesinde yerine yazalım: 1=a²/8+(4-a)a/8 ve buradan a=2 buluruz. Dolayısıyla b²=8 olur.
Yani elips denklemi x²+y²=8 dir. Burada hem asal eksen hem de yedek eksen uzunluğu 4√2 dir.
Aslında bu elipsin bir çember olduğu açıktır.
NOT: y=-x+4 doğrusu elipse teğet olduğuna göre elips denkleminde y yerine -x+4 yazarak elde edeceğiniz ikinci dereceden denklemin diskriminantını 0'a eşitleyerek de b değerini bulabilirdiniz.
Teğetin değme noktası (a, 4-a) olsun. Bu nokta elips üzerinde olduğuna göre elipsin denklemini sağlar.
a²/8+(4-a)²/b²=1 olmaldır. ...(I)
Verilen elips denkleminin x'e göre türevini alalım: 2x/8+2y.y'/b²=0
(a, 4-a) noktasında çizilen teğetin eğimi m=-1 olduğuna göre son denklemde x=a, y=4-a ve y'=-1 olmalıdır. Buradan
a/8+(a-4)/b²=0 ... (II) elde edilir.
(II) ifadesinden b²=8(4-a)/a bulunur. Bunu (I) ifadesinde yerine yazalım: 1=a²/8+(4-a)a/8 ve buradan a=2 buluruz. Dolayısıyla b²=8 olur.
Yani elips denklemi x²+y²=8 dir. Burada hem asal eksen hem de yedek eksen uzunluğu 4√2 dir.
Aslında bu elipsin bir çember olduğu açıktır.
NOT: y=-x+4 doğrusu elipse teğet olduğuna göre elips denkleminde y yerine -x+4 yazarak elde edeceğiniz ikinci dereceden denklemin diskriminantını 0'a eşitleyerek de b değerini bulabilirdiniz.
mathematics21 15:37 04 May 2013 #6 5) y=4x-2 doğrusuna paralel doğrular y=4x+b şeklindedir. Bu doğru verilen elipse teğet ise elips denkleminde y yerine 4x+b yazdığımızda elde edeceğimiz ikinci dereceden denklemin diskriminantı sıfır olmalıdır.
2x²+3(4x+b)²=12
2x²+3(16x²+8xb+b²)=12
50x²+24bx + 3b²-12=0
bu ifadenin diskriminantı sıfır olacağından
(24b)²-4.50.(3b²-12) = 0
24.24.b²-12.50.b²+4.12.50=0 (her tarafı 12 ye bölelim)
2.24.b²-50.b²+4.50=0
2b²=200
b=10 veya b=-10.
Yani aradığımız teğetler y = 4x+10 ve y = 4x-10 doğrularıdır.
2x²+3(4x+b)²=12
2x²+3(16x²+8xb+b²)=12
50x²+24bx + 3b²-12=0
bu ifadenin diskriminantı sıfır olacağından
(24b)²-4.50.(3b²-12) = 0
24.24.b²-12.50.b²+4.12.50=0 (her tarafı 12 ye bölelim)
2.24.b²-50.b²+4.50=0
2b²=200
b=10 veya b=-10.
Yani aradığımız teğetler y = 4x+10 ve y = 4x-10 doğrularıdır.
mathematics21 15:45 04 May 2013 #7 6) K(0, 3) noktasının elipsin üzerinde olmadığına dikkat edelim. (0, 3) noktasından geçen doğrular y=mx+3 şeklindedir. Yine elips denkleminde y yerine mx+3 yazıp diskriminantı sıfıra eşitleyelim:
x²+2(mx+3)²=2
(1+2m²)x²+12mx+16=0
diskriminant = 0 ise
(12m)²-4.(1+2m²).16=0
144m²-64(1+2m²)=0
16m²=64
m=2 veya m=-2 olur.
Yani aradığımız teğetler y = 2x+3 ve y = -2x+3 tür. (Cevabınızı kontrol edin lütfen)
x²+2(mx+3)²=2
(1+2m²)x²+12mx+16=0
diskriminant = 0 ise
(12m)²-4.(1+2m²).16=0
144m²-64(1+2m²)=0
16m²=64
m=2 veya m=-2 olur.
Yani aradığımız teğetler y = 2x+3 ve y = -2x+3 tür. (Cevabınızı kontrol edin lütfen)
mathematics21 15:56 04 May 2013 #8 7) Çizdiğiniz şekle göre asal eksen ve yedek eksen belli olmamakla birlikte biz birini düşünüp yapalım:
Merkezi orijin olduğuna göre elipsin denklemi x²/a²+y²/b²=1 dir. Eksenlerden birinin uzunluğu 4√3 diğerinin uzunluğu 2 olduğuna göre a ve b sayılarından biri 2√3 diğeri 1 dir. a=2√3 ve b=1 alalım: Bu durumda asal eksenin x ekseni olduğunu kabul etmiş oluyoruz.
Elips denklemi x²/12+y²=1 dir. Yine aradığımız teğetler y = -2x + b şeklinde olmalıdır. Bunu elipsin denkleminde yerine yazalım:
x²/12+(-2x+b)²=1
x²/12+4x²-4bx+b²=1
49x²/12 - 4bx + b²-1 = 0
yine diskrimininntı sıfıra eşitleyelim:
(4b)²-4.49/12.(b²-1)=0
16b²-49/3.(b²-1)=0
48b²-49(b²-1)=0
b²=49
b=7 veya b=-7 olur.
Teğetler y = -2x + 7 veya y = -2x - 7 dir. Bu teğetlerin x eksenini kestiği noktaların apsisi x = 7/2 ve x=-7/2 dir.
Merkezi orijin olduğuna göre elipsin denklemi x²/a²+y²/b²=1 dir. Eksenlerden birinin uzunluğu 4√3 diğerinin uzunluğu 2 olduğuna göre a ve b sayılarından biri 2√3 diğeri 1 dir. a=2√3 ve b=1 alalım: Bu durumda asal eksenin x ekseni olduğunu kabul etmiş oluyoruz.
Elips denklemi x²/12+y²=1 dir. Yine aradığımız teğetler y = -2x + b şeklinde olmalıdır. Bunu elipsin denkleminde yerine yazalım:
x²/12+(-2x+b)²=1
x²/12+4x²-4bx+b²=1
49x²/12 - 4bx + b²-1 = 0
yine diskrimininntı sıfıra eşitleyelim:
(4b)²-4.49/12.(b²-1)=0
16b²-49/3.(b²-1)=0
48b²-49(b²-1)=0
b²=49
b=7 veya b=-7 olur.
Teğetler y = -2x + 7 veya y = -2x - 7 dir. Bu teğetlerin x eksenini kestiği noktaların apsisi x = 7/2 ve x=-7/2 dir.
mathematics21 16:05 04 May 2013 #9 8) Bu soruyu en başta okusam belki yukarıda yazdıklarımın bazıları değişebilirdi. Türev biliyoruz yani. Ayrıca yerine koyma dışında şöyle de yapabiliriz.
Teğetin elipse değme noktası (a, 2a+n) olsun. Teğetin eğimi 2 olduğuna göre türev aldıktan sonra y'=2 olmalıdır.
Şimdi elips denklemini x²+4y²=8 şeklinde düzenleyip türev alalım:
2x+8yy'=0
2a+8(2a+n).2=0
17a+8n=0
n=-17a/8 ... (I)
Ayrıca (a, 2a+n) noktası elipsin üzerinde olduğuna göre a²+4(2a+n)²=8 olur. n yerine -17a/8 yazalım:
a²+4(2a-17a/8)²=8
a²+4(-a/8)²=8
a²+a²/16=8
17a²=16.8
34a²=16.16
a=16/√34 veya a= -16/√34 buluruz.
Bu durumda
n=√34 veya n= -√34 olur.
Teğetin elipse değme noktası (a, 2a+n) olsun. Teğetin eğimi 2 olduğuna göre türev aldıktan sonra y'=2 olmalıdır.
Şimdi elips denklemini x²+4y²=8 şeklinde düzenleyip türev alalım:
2x+8yy'=0
2a+8(2a+n).2=0
17a+8n=0
n=-17a/8 ... (I)
Ayrıca (a, 2a+n) noktası elipsin üzerinde olduğuna göre a²+4(2a+n)²=8 olur. n yerine -17a/8 yazalım:
a²+4(2a-17a/8)²=8
a²+4(-a/8)²=8
a²+a²/16=8
17a²=16.8
34a²=16.16
a=16/√34 veya a= -16/√34 buluruz.
Bu durumda
n=√34 veya n= -√34 olur.
Sevgili hocam,
Çözümlerin her biri çok anlaşılır, çok güzeller... Renklendirme de öyle... Vakit ayırdığınız için varın sağ olun; emeğinize sağlık, aklınıza âfiyet...
Çözümlerin her biri çok anlaşılır, çok güzeller... Renklendirme de öyle... Vakit ayırdığınız için varın sağ olun; emeğinize sağlık, aklınıza âfiyet...