S1) Eda 15 saatte bir , Ceren 10 saatte bir internete girmektedir. Cereb ile Eda ilk kez birlikte Cuma günü saat 16:00 da internete girmiştir.
Eda ile Ceren 13. kez beraber girdiklerinde hangi gün , saaç kaç olur?
(cevap : cumartesi , 16 : 00 )
(Ben Pazrtesi 16:00 buluyorum..... benmi yanlış buluyorum acaba ?)
S2) 67 = 3 (mod m) denkliğini sağlayan kaç tane m doğal sayısı vardır?
(cevap : 6 )
(ben 7 buluyorum cevap mı yanlış , benmi yanlış buluyorum acaba ? )
S3) Bir sınıfta K dersinden geçen L dersinden , M dersinden geçen ise K dersinden kalmıştır.
K dersinden geçen 10 kişi , L dersinden geçen 7 kişi , M dersinden geçen 12 kişi ve yanlız bir dersden geçen 27 kişi olduğuna göre L ve M dersinin her ikisinden kaç kişi geçmiştir?
(cevap : 1)
S4) En az bir dil bilenlerin bulunduğu bir sınıfta Almanca bilenler Fransızca , Fransızca bilenler de İngilizce bilmektedir. Almanca bilmeyenlerin sayısı 16, fransızca bilenlerin sayısı 20 , her üç dili bilenler ile sadece ingilizce bilenlerin toplamı 22 dir ... Buna göre sadece ingilizce bilen kaç öğrenci vardır?
(cevap : 9 )
S5) Almanca ve ingilizce dillerini bilen ve bilmeyen öğrencilerin bulunduğu sınıfın % 60 ını , iki dilide bilmeyenler sınıfın % 15 ini , ingilizce bilenler sınıfın % 30 unu oluşturmaktadır. Bu sınıfta sadece Almanca bilenler 11 kişi olduğuna göre sınıfın mevcudu kaçtır?
(cevap : 20)
Eda ile Ceren 13. kez beraber girdiklerinde hangi gün , saaç kaç olur?
(cevap : cumartesi , 16 : 00 )
(Ben Pazrtesi 16:00 buluyorum..... benmi yanlış buluyorum acaba ?)
S2) 67 = 3 (mod m) denkliğini sağlayan kaç tane m doğal sayısı vardır?
(cevap : 6 )
(ben 7 buluyorum cevap mı yanlış , benmi yanlış buluyorum acaba ? )
S3) Bir sınıfta K dersinden geçen L dersinden , M dersinden geçen ise K dersinden kalmıştır.
K dersinden geçen 10 kişi , L dersinden geçen 7 kişi , M dersinden geçen 12 kişi ve yanlız bir dersden geçen 27 kişi olduğuna göre L ve M dersinin her ikisinden kaç kişi geçmiştir?
(cevap : 1)
S4) En az bir dil bilenlerin bulunduğu bir sınıfta Almanca bilenler Fransızca , Fransızca bilenler de İngilizce bilmektedir. Almanca bilmeyenlerin sayısı 16, fransızca bilenlerin sayısı 20 , her üç dili bilenler ile sadece ingilizce bilenlerin toplamı 22 dir ... Buna göre sadece ingilizce bilen kaç öğrenci vardır?
(cevap : 9 )
S5) Almanca ve ingilizce dillerini bilen ve bilmeyen öğrencilerin bulunduğu sınıfın % 60 ını , iki dilide bilmeyenler sınıfın % 15 ini , ingilizce bilenler sınıfın % 30 unu oluşturmaktadır. Bu sınıfta sadece Almanca bilenler 11 kişi olduğuna göre sınıfın mevcudu kaçtır?
(cevap : 20)
S2) 67 = 3 (mod m) denkliğini sağlayan kaç tane m doğal sayısı vardır?
m ile bölündüğünde 3 kalanını veren sayıları arıyoruz.
m/3 = m.k+3 => mk+3
67=mk+3
64=m.k
Şöyle düşndüm 67 ile bölündüğünde 3 kalanı veren sayıları aramamız demek 64 ile tam bölünen sayıları aramamız gibi olur.Bunlar 1.64 , 32.2 , 16.4 , 8.8 , 4.16 , 2.32 , 64.1 olur.Bunu sağlayan sayılarda 7 tanedir.Eğer ekstra bir şart verilmediyse.
Tamam ya böyle olması gerekiyor.Denersende görürsün zaten.
Kusura bakma , tatildeyim Bir bakayım dedim forumumuz ne alemde ? 3 -4 gün sonra hep forumda olacağım.O zaman yardımcı olmaya çalışacam(Ben gelene kadar çoktan çözülür ama )
Bir bakayım dedim forumumuz ne alemde ? 3 -4 gün sonra hep forumda olacağım.O zaman yardımcı olmaya çalışacam(Ben gelene kadar çoktan çözülür ama ) 
m ile bölündüğünde 3 kalanını veren sayıları arıyoruz.
m/3 = m.k+3 => mk+3
67=mk+3
64=m.k
Şöyle düşndüm 67 ile bölündüğünde 3 kalanı veren sayıları aramamız demek 64 ile tam bölünen sayıları aramamız gibi olur.Bunlar 1.64 , 32.2 , 16.4 , 8.8 , 4.16 , 2.32 , 64.1 olur.Bunu sağlayan sayılarda 7 tanedir.Eğer ekstra bir şart verilmediyse.
Tamam ya böyle olması gerekiyor.Denersende görürsün zaten.
Kusura bakma , tatildeyim
S2) 67 = 3 (mod m) denkliğini sağlayan kaç tane m doğal sayısı vardır?
m ile bölündüğünde 3 kalanını veren sayıları arıyoruz.
m/3 = m.k+3 => mk+3
67=mk+3
64=m.k
m k
1 64
2 32
4 16
8 8
64 1
32 2
16 4
Görüldüğü gibi 7 tane var.(Ve yerine koyarsak sağlıyor zaten) Eğer bu şekildeyse 7 tane olmalı.6 tane olması için ancak m>1 veya m≠k şeklinde bir şart verilmesi gereklidir.Böyle bir şart yazmayı unutmuşlar.Böyle olmalı.
M = Bölen
K=Bölüm
m ile bölündüğünde 3 kalanını veren sayıları arıyoruz.
m/3 = m.k+3 => mk+3
67=mk+3
64=m.k
m k
1 64
2 32
4 16
8 8
64 1
32 2
16 4
Görüldüğü gibi 7 tane var.(Ve yerine koyarsak sağlıyor zaten) Eğer bu şekildeyse 7 tane olmalı.6 tane olması için ancak m>1 veya m≠k şeklinde bir şart verilmesi gereklidir.Böyle bir şart yazmayı unutmuşlar.Böyle olmalı.
M = Bölen
K=Bölüm
bende öyle buldum cevap yanlış o zaman
diğerleri için fikrin var mı hocam
1)


2)


3)


4)


5)

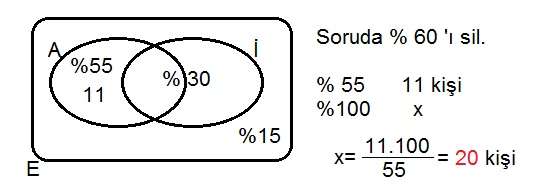
Sanırım hatamızın ne olduğunu anladım mod 1'e göre olursa 64'ün 1 ile bölümünden kalan 0 olacaktır.
(Kusurabakma tatildeyiz.Tam bakamadım.)
(Kusurabakma tatildeyiz.Tam bakamadım.)
hocam günü bulmak için 7 ye bölmüyormuyuz ? o zaman farklı çıkıyor sonuç ...
