Yardımcı olursanız sevinirim.
Kolay gelsin.
gereksizyorumcu 16:04 04 Ağu 2012 #2
1.
simetrik olduğundan üst yarıya bakalım
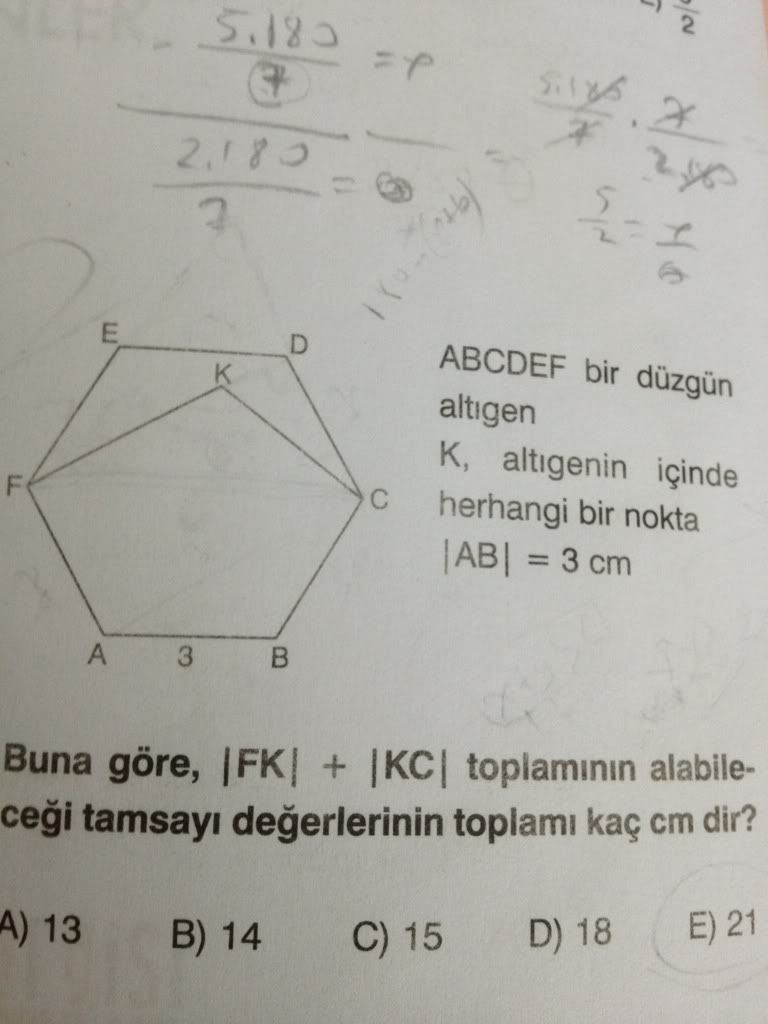
FKC üçgenine baktığımızda K FC nin üzerinde olsa bile toplam en az 6 olabilir.
FEDC nin uzunluğu da 9 olduğuna göre FK+KC toplamı bundan küçük olmalıdır (şekiller konveks ve FEDC FKC yolunu dıştan kapsıyor aynı yerden başlayıp aynı yerde bitiyorlar)
kısaca 6≤toplam<9 bulunur. peki bu değerleri alabilir mi? K yı tam E noktasında seçersek toplam 3.(√3+1)>8 oluyor ki bu da yeterli
alınan değerler toplamı 6+7+8=21 olur.
2.
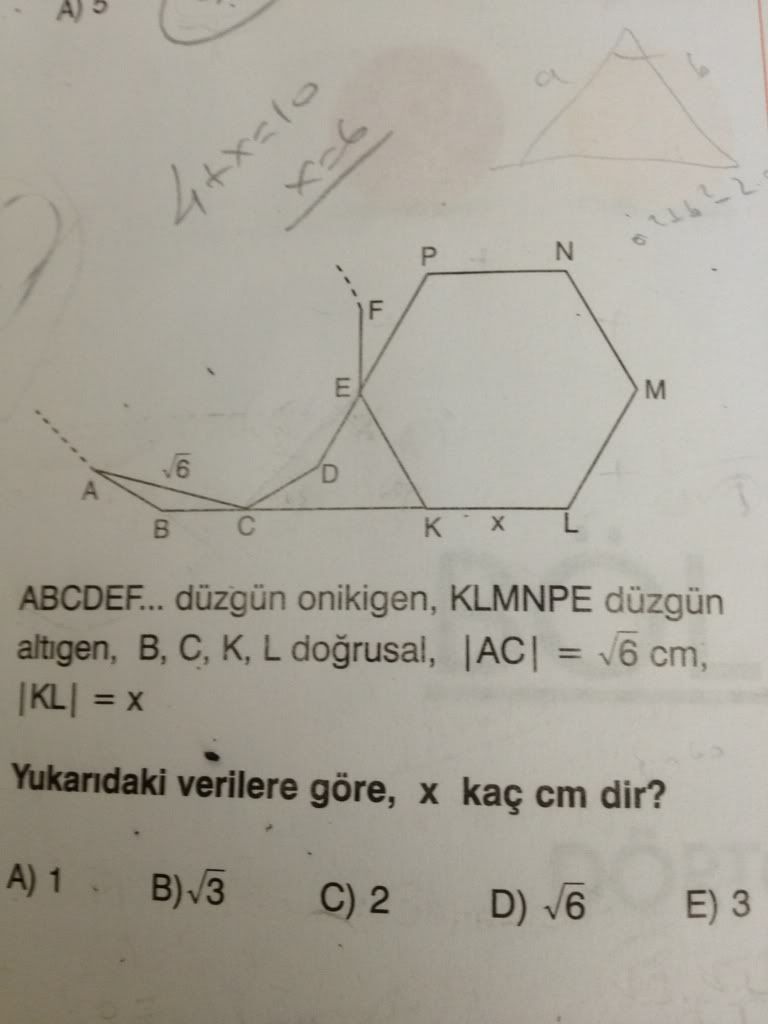
CE yi yaptığınız gibi birleştirip E den de CK ya dik inilirse dikmenin uzunluğu √3 bulunur , x=2 bulunur
3.
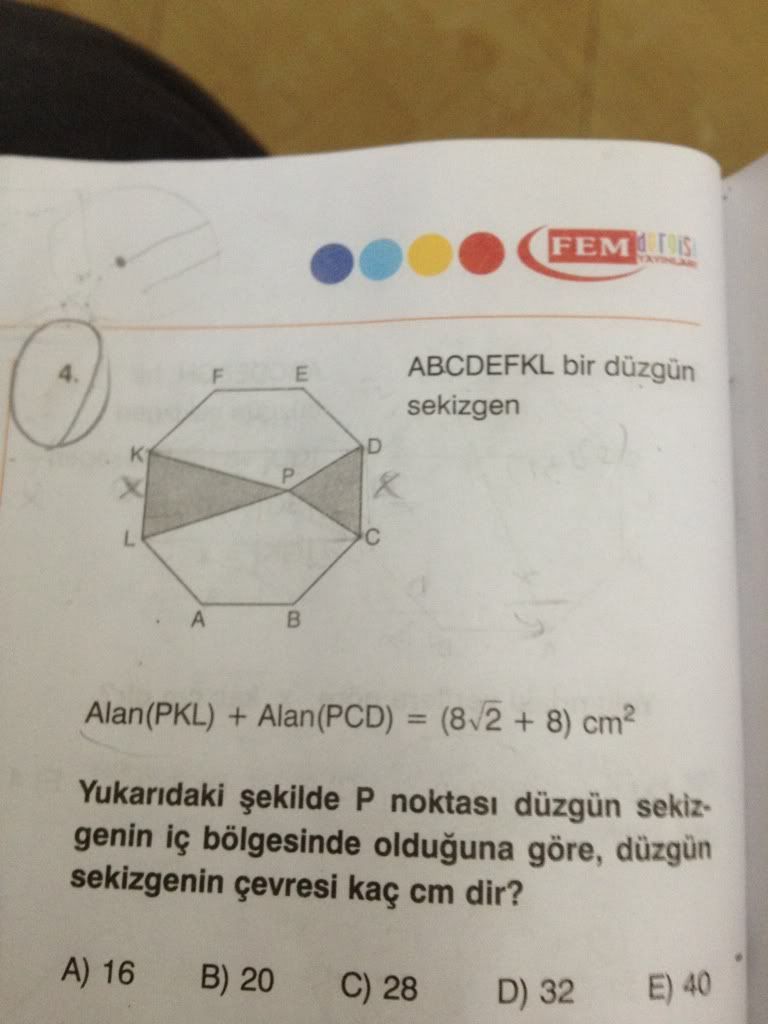
KD bu iki üçgenin toplam yüksekliğidir. ayrıca KD=x(1+√2) uzunluğundadır.
alan=x.(x(1+√2))/2=8+8√2 verilmiş , x=4 bulunur
çevre 32 olur
simetrik olduğundan üst yarıya bakalım
FKC üçgenine baktığımızda K FC nin üzerinde olsa bile toplam en az 6 olabilir.
FEDC nin uzunluğu da 9 olduğuna göre FK+KC toplamı bundan küçük olmalıdır (şekiller konveks ve FEDC FKC yolunu dıştan kapsıyor aynı yerden başlayıp aynı yerde bitiyorlar)
kısaca 6≤toplam<9 bulunur. peki bu değerleri alabilir mi? K yı tam E noktasında seçersek toplam 3.(√3+1)>8 oluyor ki bu da yeterli
alınan değerler toplamı 6+7+8=21 olur.
2.
CE yi yaptığınız gibi birleştirip E den de CK ya dik inilirse dikmenin uzunluğu √3 bulunur , x=2 bulunur
3.
KD bu iki üçgenin toplam yüksekliğidir. ayrıca KD=x(1+√2) uzunluğundadır.
alan=x.(x(1+√2))/2=8+8√2 verilmiş , x=4 bulunur
çevre 32 olur
hocam öncelikle cok teşekkürler ..
1. ve 2.soruyu şekil ile izah edebilirmisiniz?
1. ve 2.soruyu şekil ile izah edebilirmisiniz?
edit ;
1.soruyu algılamak kaldı..
1.soruyu algılamak kaldı..
yazdığın açı yanlış orası 30 değil 45 olacak
böyle bir hatayı nasıl yapmışım 
150 dereceyi tek bir kısım olarak algılamışım..
gözle görünür bende 30 derece olarak kabul edemiyordum zaten
sagol orkun.
150 dereceyi tek bir kısım olarak algılamışım..gözle görünür bende 30 derece olarak kabul edemiyordum zaten
sagol orkun.
hocam ben ilk soruda ne demek istediğinizi anladım fakat anlamadığım yer FK+KC maks değerini E nin ya da D nin üstündeyken mi alıyor?
gereksizyorumcu 06:18 05 Ağu 2012 #8 hocam ben ilk soruda ne demek istediğinizi anladım fakat anlamadığım yer FK+KC maks değerini E nin ya da D nin üstündeyken mi alıyor?
öncelikle noktanın FE ve DC üzerinde olduğunda noktayı E veya D ye çekmenin üçgen eşitsizliğine göre FK+KC yi kesinlikle büyüteceği tespiti yapılır.
artık noktanın DE arasında olduğu kesin
K dan FC ye dik inilir , ayırdığı parçalar x ve (6-x) olur , yüksekliği ise 3√3/2
(FK)²=x²+27/4
(KC)²=(6-x)²+27/4
işte buna göre türev alınırsa
x=3/2 yani D veya x=9/2 yani E noktalarında max olduğu bulunur