karışık sorular-2

mrs.nobody 19:53 18 Mar 2012 #1

1) A={x|x=4k, k∈Z,15<x<115}
B={x|x=6k, k∈Z,30<x<130}
olduğuna göre, (A-B)∪(B-A) kümesinin eleman sayısı kaçtır?
a)39
b)36
c)33
d)30
e)27
[cevap E]

2)Birbirinden farklı iki basamaklı 4 pozitif tam sayının alabileceği değerlerin toplamı A ise,A kaç farklı değer alabilir?
a)200
b)240
c)244
d)340
e)345
[cevap E]

3)Şampiyonlar ligi maçlarında galibiyete 2 milyon dolar,beraberliğe 1 milyon dolar veriliyor.Yeniden takıma para verilmiyor.Her takım diğer takımlarla ikişer defa karşılaşıyor.
Lig sonunda toplam 112 milyon dolar dağıtılmış olduğuna göre,bu ligde kaç takım vardır?
a)4
b)6
c)8
d)10
e)12
[cevap C]

4)Bir kuruyemişçi kilogramını 25 TL ye aldığı bademin kilogramını 32 TL ye satıyor.Satıştan sonra terazinin hatalı olduğunu ve %25 fazla gösterdiğini tespit ediyor.
Buna göre,kuruyemişçinin badem satışından elde ettiği gerçek kar oranı yüzde kaçtır?
a)40
b)50
c)60
d)70
e)80
[cevap C]

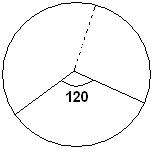
5)

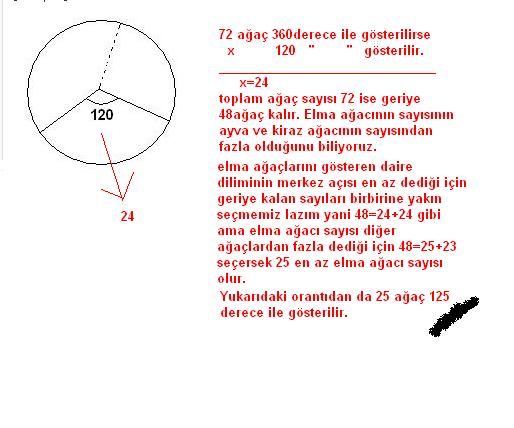
Yukarıdaki dairesel grafik,sadece kiraz,elma ve ayva ağaçlarının bulunduğu bir bahçedeki ağaçların dağılımını göstermektedir.Bahçedeki elma ağaçlarının sayısı,kiraz ve ayva ağaçlarının sayısından fazladır.
Bu bahçede toplam 72 ağaç olduğuna göre,elma ağaçlarını gösteren daire diliminin merkez açısı en az kaç derece olabilir?
a)150
b)135
c)130
d)125
e)121
[cevap D]

sinavkizi 20:43 18 Mar 2012 #2

cevap 2.

A'nın en küçük ve en büyük değerlerini bulalım, sonra aradaki sayılar da gelir zaten.
2 basamaklı sayılar: (10,11,12,13..........96,97,98,99)

A en küçük: (10+11+12+13=46) olur. A'nın alabileceği değerler 46'dan başlar.
A en büyük: (99+98+97+96)=390) olur. A'nın alabileceği değer en son 390'da biter.

(46,47,48..........390)'a kadar kaç sayı var'ı arıyoruz, o da terim sayısı:
[(son terim-ilk terim)/artma miktarı]+1=[(390-46)/1]+1=345.

Buna benzer bir soru 2005'te çıkmıştı. (bkz: http://www.lysmat.com/snv/mat/2005_oss/c11.gif?psid=1)