1) Doğrusal bir yolda,bir otomobil sabit hızla belli bir yolun yarısını 5 saatte alıyor ve 1 saat mola veriyor.Başlangıçtaki hızıyla tekrar yola çıkıp her saatte hızını 10 km/saat artırarak yolu tamamlıyor.
Yolculuk toplam 9 saatte tamamlandığına göre,otomobilin en son hızı kaç km/saattir?
a)25
b)35
c)40
d)45
e)50
[cevap B]
2) Hergün evden okula sabit bir hızla ve aynı sürede giden bir öğrenci,yine okula gitmek için yola çıkıyor.Yolun 3/5 ini gittikten sonra evde birşey unuttuğunu fark ediyor.
Hızını % kaç arttırırsa,kalan sürede eve dönüp alacağını aldıktan sonra okula yetişir?
a)200
b)250
c)300
d)350
e)400
[cevap C]
3)
7V₁=3V₂ olmak üzere,yukarıdaki şekilde B den aynı anda A ya doğru harekete başlayan iki hareketli A ve C arasında sürekli gidip gelmektedir.
2.karşılaşmaları B noktasında gerçekleştiğine göre |BC|/|AC| oranı kaçtır?
a)4/7
b)3/5
c)5/7
d)2/3
e)3/4
[cevap A]
4)
Yukarıdaki şekilde,bir bankanın vadeli hesaplara uygulayacağı faiz oranlarını belirleyen bir fonksiyonun grafiği verilmiştir.
Bu grafiğe göre,kaçıncı yıldan sonra yıllık faiz oranı %10 un altına düşer?
a)8
b)9
c)10
d)11
e)12
[cevap E]
5)
olduğuna göre, toplamı kaçtır?
toplamı kaçtır?
a)1/2
b)2
c)1
d)5/2
e)3
[cevap B]
Yolculuk toplam 9 saatte tamamlandığına göre,otomobilin en son hızı kaç km/saattir?
a)25
b)35
c)40
d)45
e)50
[cevap B]
2) Hergün evden okula sabit bir hızla ve aynı sürede giden bir öğrenci,yine okula gitmek için yola çıkıyor.Yolun 3/5 ini gittikten sonra evde birşey unuttuğunu fark ediyor.
Hızını % kaç arttırırsa,kalan sürede eve dönüp alacağını aldıktan sonra okula yetişir?
a)200
b)250
c)300
d)350
e)400
[cevap C]
3)
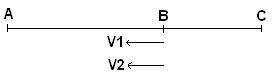
7V₁=3V₂ olmak üzere,yukarıdaki şekilde B den aynı anda A ya doğru harekete başlayan iki hareketli A ve C arasında sürekli gidip gelmektedir.
2.karşılaşmaları B noktasında gerçekleştiğine göre |BC|/|AC| oranı kaçtır?
a)4/7
b)3/5
c)5/7
d)2/3
e)3/4
[cevap A]
4)
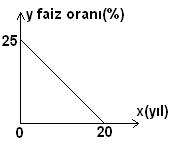
Yukarıdaki şekilde,bir bankanın vadeli hesaplara uygulayacağı faiz oranlarını belirleyen bir fonksiyonun grafiği verilmiştir.
Bu grafiğe göre,kaçıncı yıldan sonra yıllık faiz oranı %10 un altına düşer?
a)8
b)9
c)10
d)11
e)12
[cevap E]
5)
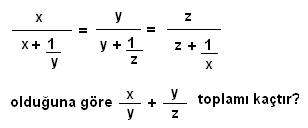
olduğuna göre,
 toplamı kaçtır?
toplamı kaçtır?a)1/2
b)2
c)1
d)5/2
e)3
[cevap B]
C.1
Yolun tamamı 2x olsun.
Yarısını yani x ini 5 saatte gitmiş. (V hız ile)
+1 saat mola vermiş.
Ve yolculuğu 9 saatte tamamlamış.
Yani moladan sonra 3 saat daha gitmiş. Ve böylece yolu tamamlamış.
Moladan sonra yolu her saat sonunda hızını 10km arttırarak gidiyormuş yani;
v,v+10,v+20 olarak gidiyormuş.Ortalama hızı=v+10
Moladan önce gittiği yol=x=5.V
Moladan sonra gittiği yol=x=3.(V+10)
5V=3V+30
V=15
Son durumdaki hızı=V+20=15+20=35
C.4
x yıl y faiz olmak üzere;
x/20+y/25=1
5x+4y=100
faiz oranı %10 ise
5x+40=100
5x=60
x=12
12 yıl sora faiz oranı %10 olur. 12 yıldan sonra faiz oranı %10 un altına iner.
Grafik sorularında analitik bilgilerini kullanmayı unutma.***
C.5
Mantıken yaptım.
x/x+1=y/y+1 ise
x=y olmalıdır.
.........
x=tek ise
x/x+1=Tek/Çift olur. Y yide bu durumda tek seçmeliyiz.
Mesela
3/4≠5/6
x/x+1 veya y/y+1 sadeleşemeyeceğinden ve başka türlü de eşit olamayacağından
x=y

Yolun tamamı 2x olsun.
Yarısını yani x ini 5 saatte gitmiş. (V hız ile)
+1 saat mola vermiş.
Ve yolculuğu 9 saatte tamamlamış.
Yani moladan sonra 3 saat daha gitmiş. Ve böylece yolu tamamlamış.
Moladan sonra yolu her saat sonunda hızını 10km arttırarak gidiyormuş yani;
v,v+10,v+20 olarak gidiyormuş.Ortalama hızı=v+10
Moladan önce gittiği yol=x=5.V
Moladan sonra gittiği yol=x=3.(V+10)
5V=3V+30
V=15
Son durumdaki hızı=V+20=15+20=35
C.4
x yıl y faiz olmak üzere;
x/20+y/25=1
5x+4y=100
faiz oranı %10 ise
5x+40=100
5x=60
x=12
12 yıl sora faiz oranı %10 olur. 12 yıldan sonra faiz oranı %10 un altına iner.
Grafik sorularında analitik bilgilerini kullanmayı unutma.***
C.5
Mantıken yaptım.
x/x+1=y/y+1 ise
x=y olmalıdır.
.........
x=tek ise
x/x+1=Tek/Çift olur. Y yide bu durumda tek seçmeliyiz.
Mesela
3/4≠5/6
x/x+1 veya y/y+1 sadeleşemeyeceğinden ve başka türlü de eşit olamayacağından
x=y

cevaplanmış görmedim. 
C.2
Yolun tamamı 10x olsun.
Hergün 10x V hız ile t sürede gidiyormuş.
Ama bugün yolun önce (3/5ini) 6xini gitmiş. Sonra geri dönerek 6x daha gitmiş. Sonra 10x daha giderek okula ulaşmış. Bu işlem sonunda 22x yol gitmiş. Ancak yine t sürede ve hızını biraz arttırarak.
10x=V.t ise
x=V.t/10
22x=22.V.t/10 Buna göre 2. durumdaki hızı 22V/10
İlk durumdaki hızı V
İkinci durumda hızını V+12V/10 ye yani 22V/10 a çıkarmış. Yani hızını ilk hızına göre 12V/10 arttırmış.
%100 V ise
%x 12V/10
x=120
Ben nerede hata yapıyorum.??
Yolun tamamı 10x olsun.
Hergün 10x V hız ile t sürede gidiyormuş.
Ama bugün yolun önce (3/5ini) 6xini gitmiş. Sonra geri dönerek 6x daha gitmiş. Sonra 10x daha giderek okula ulaşmış. Bu işlem sonunda 22x yol gitmiş. Ancak yine t sürede ve hızını biraz arttırarak.
10x=V.t ise
x=V.t/10
22x=22.V.t/10 Buna göre 2. durumdaki hızı 22V/10
İlk durumdaki hızı V
İkinci durumda hızını V+12V/10 ye yani 22V/10 a çıkarmış. Yani hızını ilk hızına göre 12V/10 arttırmış.
%100 V ise
%x 12V/10
x=120
Ben nerede hata yapıyorum.??
C.2
Yolun tamamı 10x olsun.
Hergün 10x V hız ile t sürede gidiyormuş.
Ama bugün yolun önce (3/5ini) 6xini gitmiş. Sonra geri dönerek 6x daha gitmiş. Sonra 10x daha giderek okula ulaşmış. Bu işlem sonunda 22x yol gitmiş. Ancak yine t sürede ve hızını biraz arttırarak.
10x=V.t ise
x=V.t/10
22x=22.V.t/10 Buna göre 2. durumdaki hızı 22V/10
İlk durumdaki hızı V
İkinci durumda hızını V+12V/10 ye yani 22V/10 a çıkarmış. Yani hızını ilk hızına göre 12V/10 arttırmış.
%100 V ise
%x 12V/10
x=120
Ben nerede hata yapıyorum.??
Yolun tamamı 10x olsun.
Hergün 10x V hız ile t sürede gidiyormuş.
Ama bugün yolun önce (3/5ini) 6xini gitmiş. Sonra geri dönerek 6x daha gitmiş. Sonra 10x daha giderek okula ulaşmış. Bu işlem sonunda 22x yol gitmiş. Ancak yine t sürede ve hızını biraz arttırarak.
10x=V.t ise
x=V.t/10
22x=22.V.t/10 Buna göre 2. durumdaki hızı 22V/10
İlk durumdaki hızı V
İkinci durumda hızını V+12V/10 ye yani 22V/10 a çıkarmış. Yani hızını ilk hızına göre 12V/10 arttırmış.
%100 V ise
%x 12V/10
x=120
Ben nerede hata yapıyorum.??
yolun 6x ini V hızıyla gitmiş------> V₁.t=6x
eve geri dönüp tekrar okula gittiğinde aldığı yol 16 x olur.-----> V₂.t=16x
buradan V₂'yi 8/3 V₁ buluruz.
orantıdan-------> 1 de 5/3 arttırdıysa
100de 500/3 arttırmıştır.
Verdiğin yol değerleri yanlış.
Sen yolun ilk başta 5/3 ünü almışsın. Ama soruda 3/5i diyor.
Sen yolun ilk başta 5/3 ünü almışsın. Ama soruda 3/5i diyor.
3)

1.Karşılaşma [AB] arasında, 2.karşılaşma B noktasında.
2.Karşılaşma anına kadar iki hareketlide zaman aynıdır.
7.2y=3((2x+2y)
14y=6x+6y
8y=6x
x=4k
y=3k
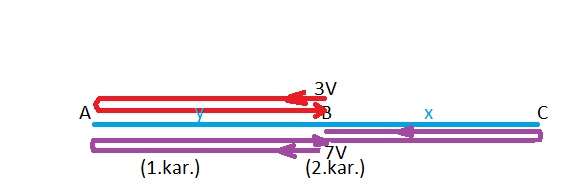
1.Karşılaşma [AB] arasında, 2.karşılaşma B noktasında.
zaman=
yol
hız
2.Karşılaşma anına kadar iki hareketlide zaman aynıdır.
t=
y+y
3V
=
y+y+x+x
7V
7.2y=3((2x+2y)
14y=6x+6y
8y=6x
x=4k
y=3k
|BC|
|AC|
=
x
x+y
=
4k
7k
=
4
7
Verdiğin yol değerleri yanlış.
Sen yolun ilk başta 5/3 ünü almışsın. Ama soruda 3/5i diyor.
Sen yolun ilk başta 5/3 ünü almışsın. Ama soruda 3/5i diyor.
yolun tamamı 5x olsun V hızıyla 5t sürede bu yolu alsın.Yani 5x=V.5t
evde birşeyini unutmadan önce 3x yol gitmiş. 3x=V.3t olduğundan 3t süresini kullanmış. 5t-3t=2t sürede 3x+5x=8x yol alması gerek.
V₂.2t=8x
buradan V₂=4V bulunur.
v de 3v artmış
100 de 300 artar.
emeklerinize sağlık teşekkür ederim 
şöyle yapınca oluyor sanırım:
yolun tamamı 5x olsun V hızıyla 5t sürede bu yolu alsın.Yani 5x=V.5t
evde birşeyini unutmadan önce 3x yol gitmiş. 3x=V.3t olduğundan 3t süresini kullanmış. 5t-3t=2t sürede 3x+5x=8x yol alması gerek.
V₂.2t=8x
buradan V₂=4V bulunur.
v de 3v artmış
100 de 300 artar.
yolun tamamı 5x olsun V hızıyla 5t sürede bu yolu alsın.Yani 5x=V.5t
evde birşeyini unutmadan önce 3x yol gitmiş. 3x=V.3t olduğundan 3t süresini kullanmış. 5t-3t=2t sürede 3x+5x=8x yol alması gerek.
V₂.2t=8x
buradan V₂=4V bulunur.
v de 3v artmış
100 de 300 artar.
