varoluscu_prens 01:44 15 May 2012 #1
Soru çözümünde problem yaşadığım iki soru alttadır.
1-) ( 1+2/3 ) x ( 1+1/2 ) x (1+2/5) x (1+1/3) x ... x (1 + 1/6) = ?
Burada sadeleştirme paternini bulamadım. Yani parantez içini hesaplarsak ;
5 3 7 4
_ _ _ _ ... ve .7 bölü 6
3 2 5 3
bu noktada kimle kimi sadeleştireceğiz?
2-) 3/11 + 4/7 + 11/27 = x olduğuna göre;
1/11 + 3/27 + 8/7 'nin x cinsinden değeri nedir?
bu soruda güzel bir çözüm yolu bilen var mı, çakallık yapmadan çözecek biri?
teşekkür.
1-) ( 1+2/3 ) x ( 1+1/2 ) x (1+2/5) x (1+1/3) x ... x (1 + 1/6) = ?
Burada sadeleştirme paternini bulamadım. Yani parantez içini hesaplarsak ;
5 3 7 4
_ _ _ _ ... ve .7 bölü 6
3 2 5 3
bu noktada kimle kimi sadeleştireceğiz?
2-) 3/11 + 4/7 + 11/27 = x olduğuna göre;
1/11 + 3/27 + 8/7 'nin x cinsinden değeri nedir?
bu soruda güzel bir çözüm yolu bilen var mı, çakallık yapmadan çözecek biri?
teşekkür.
gereksizyorumcu 11:51 15 May 2012 #3
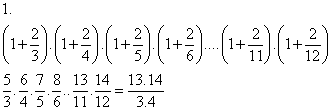
ikinci soru için seçenekleri verebilir misiniz? en azından nasıl bir yol izlendiğini görebiliriz. bu arada eliniz değmişken sorunun yazımında hata olup olmadığını da kontrol eder misiniz?
gereksizyorumcu 12:37 15 May 2012 #4
iş inada binerse şöyle bi çözüm yapabiliriz (tabi bu hesaplamaktan uzun sürer orası ayrı 
)
sorulan ifade y olduğunda
k.x+y ifadesini tamsayı yapan bi k buluruz
mod(4k,7)=6 , mod(3k,11)=10 , mod(11k,27)=24 - Wolfram|Alpha
burada n=0 seçersek k=579 un bunu sağladığı görülür.
sonuçta da 579x+y=726 olacağından
y=726-579x elde edilir.
benzer şekilde y=1500x-1876 sonuçlarına da ulaşılabilir
)sorulan ifade y olduğunda
k.x+y ifadesini tamsayı yapan bi k buluruz
mod(4k,7)=6 , mod(3k,11)=10 , mod(11k,27)=24 - Wolfram|Alpha
burada n=0 seçersek k=579 un bunu sağladığı görülür.
sonuçta da 579x+y=726 olacağından
y=726-579x elde edilir.
benzer şekilde y=1500x-1876 sonuçlarına da ulaşılabilir
iş inada binerse şöyle bi çözüm yapabiliriz (tabi bu hesaplamaktan uzun sürer orası ayrı )
sorulan ifade y olduğunda
k.x+y ifadesini tamsayı yapan bi k buluruz
mod(4k,7)=6 , mod(3k,11)=10 , mod(11k,27)=24 - Wolfram|Alpha
burada n=0 seçersek k=579 un bunu sağladığı görülür.
sonuçta da 579x+y=726 olacağından
y=726-579x elde edilir.
benzer şekilde y=1500x-1876 sonuçlarına da ulaşılabilir
)sorulan ifade y olduğunda
k.x+y ifadesini tamsayı yapan bi k buluruz
mod(4k,7)=6 , mod(3k,11)=10 , mod(11k,27)=24 - Wolfram|Alpha
burada n=0 seçersek k=579 un bunu sağladığı görülür.
sonuçta da 579x+y=726 olacağından
y=726-579x elde edilir.
benzer şekilde y=1500x-1876 sonuçlarına da ulaşılabilir
gereksizyorumcu 12:46 15 May 2012 #6 Güzel çözüm
neyse artık seçenekler verilirse ne istenildiğini kestirerek uygun bişeyler bulabiliriz
varoluscu_prens 13:32 15 May 2012 #7
Çakallık yapmamak derken bunu kastediyordum
şıklar şöyle:
soruyu düzgün olarak tekrar yazayım, kesirin nasıl yazıldığını çözdüm:
x eşittir
ise
nin x cinsinden değeri nedir?
şıklar şöyle:
4+7x
2
4-7x
2
4-3x
2
3x-2
4
4x-7
3
soruyu düzgün olarak tekrar yazayım, kesirin nasıl yazıldığını çözdüm:
x eşittir
3
11
+
4
7
+
11
27
ise
1
11
+
3
27
+
8
7
nin x cinsinden değeri nedir?
x=(3/11)+(4/7)+(11/27)
y=(1/11)+(8/7)+(3/27)
Şıklarda geçen xlerin katsayılı hallerini bulalım;
3x=(9/11)+(12/7)+(33/27)
4x=(12/11)+(16/7)+(44/27)
7x=(21/11)+(28/7)+(77/27)
Şıklarda geçen ylerin katsayılı hallerini bulalım;
2y=(2/11)+(6/27)+(16/7)
3y=(3/11)+(9/27)+(24/7)
4y=(4/11)+(12/27)+(32/7)
Seçeneklerde 4y,3y ve 2yli şıklar var.
4y'li seçeneği ele alırsak(Paydası 4 olan şık) 9/11'den 4/11'e tam sayı kullanarak ulaşamayız.
3y'li seçeneği ele alırsak(Paydası 3 olan şık) 12/11'den 3/11'e tam sayı kullanarak ulaşamayız.
2y'li şıklar için (Paydasında 2 bulunan şıklar) 2/11 sayısına sadece 9/11 ile yani;3x ile ulaşabiliriz.
1-(9/11)=2/11
4-(12/7)=16/7
(33/27)-1=6/27
________________
4-3x=2y
Olduğu görülüyor. Seçenekli ve bu kadar karışık bir soruda çok vakit kaybettirmeyen bir yöntem olduğunu düşünüyorum. Genelde şıklardan gitme yolunu kullanmam. Kullanmayı da sevmem fakat bazı sorularda şıklardan gitmek ciddi anlamda vakit kazandırabiliyor. Sonuç olarak bu da bir çözüm yolu.
y=(1/11)+(8/7)+(3/27)
Şıklarda geçen xlerin katsayılı hallerini bulalım;
3x=(9/11)+(12/7)+(33/27)
4x=(12/11)+(16/7)+(44/27)
7x=(21/11)+(28/7)+(77/27)
Şıklarda geçen ylerin katsayılı hallerini bulalım;
2y=(2/11)+(6/27)+(16/7)
3y=(3/11)+(9/27)+(24/7)
4y=(4/11)+(12/27)+(32/7)
Seçeneklerde 4y,3y ve 2yli şıklar var.
4y'li seçeneği ele alırsak(Paydası 4 olan şık) 9/11'den 4/11'e tam sayı kullanarak ulaşamayız.
3y'li seçeneği ele alırsak(Paydası 3 olan şık) 12/11'den 3/11'e tam sayı kullanarak ulaşamayız.
2y'li şıklar için (Paydasında 2 bulunan şıklar) 2/11 sayısına sadece 9/11 ile yani;3x ile ulaşabiliriz.
1-(9/11)=2/11
4-(12/7)=16/7
(33/27)-1=6/27
________________
4-3x=2y
Olduğu görülüyor. Seçenekli ve bu kadar karışık bir soruda çok vakit kaybettirmeyen bir yöntem olduğunu düşünüyorum. Genelde şıklardan gitme yolunu kullanmam. Kullanmayı da sevmem fakat bazı sorularda şıklardan gitmek ciddi anlamda vakit kazandırabiliyor. Sonuç olarak bu da bir çözüm yolu.
Çakallık yapmamak derken bunu kastediyordum
şıklar şöyle:
soruyu düzgün olarak tekrar yazayım, kesirin nasıl yazıldığını çözdüm:
x eşittir
ise
nin x cinsinden değeri nedir?
şıklar şöyle:
4+7x
2
4-7x
2
4-3x
2
3x-2
4
4x-7
3
soruyu düzgün olarak tekrar yazayım, kesirin nasıl yazıldığını çözdüm:
x eşittir
3
11
+
4
7
+
11
27
ise
1
11
+
3
27
+
8
7
nin x cinsinden değeri nedir?
Bu soruları göz kararı çözeceksiniz, n'yle çarparsam ve toplarsam tamsayı veya benzeri (sade) bir form elde edebilirim gibisinden:
1
11
+
3
27
+
8
7
= y
2
11
+
6
27
+
16
7
= 2y
9
11
+
12
7
+
33
27
= 3x
2y+3x işlemi yapılırsa 3 kesirli terimden ikisi tamsayı olur:
2y+3x=5+(39/27)=58/9 ----> y=(29/9) - (3x/2) bulunur. Anlaşılacağı üzere, soruda verilen şıklar tamamen yanlıştır!
gereksizyorumcu 15:12 15 May 2012 #10
şimdi
4-3x=2y
mi bulduk?
x ve y nin 1 ile 1.5 arasında sayılar olduğunu düşünerek seçeneklere bi daha bakalım bence
4-3x=2y
mi bulduk?
x ve y nin 1 ile 1.5 arasında sayılar olduğunu düşünerek seçeneklere bi daha bakalım bence