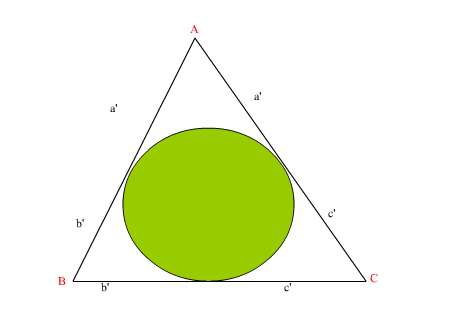
Teorem.Bir üçgende yukarıdaki gibi a',b',c' yarıçaplı çemberler çizilirse,
Alan=√a'b'c'(a'+b'+c')
bağıntısı elde edilir.
İspat.
Elimizde ne bir açı ne bir diklik var.İkisi de yok.Bakacak halimizde yok! Akıllarıza hemen heron formülü gelmeli , gelmediyse gelmiş oldu!
a',b',c' değerlerini bilmemiz demek bizim üçgenin üç kenarını da bilmemiz demektir.
Şimdi şuna bir göz atın-aslında açıortayın bölme oranı şeklinde bir konu açıp bunu da kanıtlayacağım ama işlem gereği kanıtlamaya gerek kalmadan şunu çıkarabiliriz;
u-a=(a'+b'+c')-(b'+c')=a'
u-b=(a'+b'+c')-(c'+a')=b'
u-c=(a'+b'+c')-(a'+b')=c'
Sarılacivertli ifadeler apaçık heron formülünü işaret ediyor.
Derhal yerine yazalım.
|ABC|=√u.(u-a)(u-b)(u-c) şeklinde yerine yazarsak ispatımızı tamamlamış oluruz.
Şimdiyse bu teoremle ilgili bir örnek çözelim.Olsun bitsin!
Örnek.

ABC bir üçgen D,E,F teğet değme noktaları
|EA|=2 br
|FB|=3 br
|DC|=x br
|ABC|=24 br² olduğuna göre x kaçtır?
Çözüm.
Daha kolay ne olabilir? Hemen yerine yazalım!
√(2.3.x).(5+x)=24 birim verilmiş buradan x'i çekersiniz değil mi?
Şununda garantisini verelim.Bu teorem şu şekillerde de çalışır ; pardon düzelteyim teğet değme varsa uygulayın bunu ama üçgeni oluşturan 6 doğru parçasının ikişer-ikişer takımlar halinde eşit uzunlukta olduğunu fark edin yoksa yandınız!

Teğet noktalarının eşitliğine dikkat!
Dipnot.şekil çizme işinde berbatımdır.Şekillerin bana ait olduğunu anlayabilirsiniz sanırım.Artık bu kadarıyla idare edin önemli olan kitabın şekli değil içeriğidir!
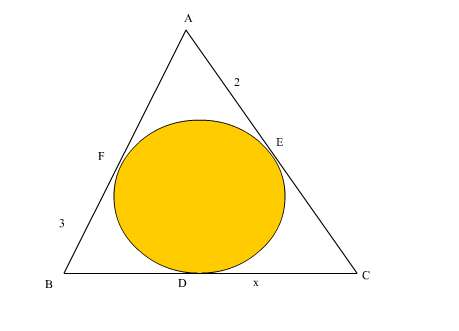
ABC bir üçgen D,E,F teğet değme noktaları
|EA|=2 br
|FB|=3 br
|DC|=x br
|ABC|=24 br² olduğuna göre x kaçtır?
Çözüm.
Daha kolay ne olabilir? Hemen yerine yazalım!
√(2.3.x).(5+x)=24 birim verilmiş buradan x'i çekersiniz değil mi?
Şununda garantisini verelim.Bu teorem şu şekillerde de çalışır ; pardon düzelteyim teğet değme varsa uygulayın bunu ama üçgeni oluşturan 6 doğru parçasının ikişer-ikişer takımlar halinde eşit uzunlukta olduğunu fark edin yoksa yandınız!
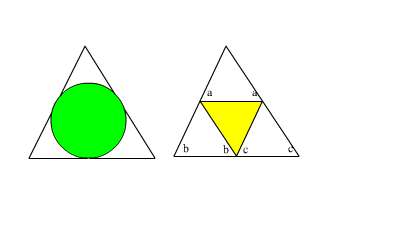
Teğet noktalarının eşitliğine dikkat!
Dipnot.şekil çizme işinde berbatımdır.Şekillerin bana ait olduğunu anlayabilirsiniz sanırım.Artık bu kadarıyla idare edin önemli olan kitabın şekli değil içeriğidir!
