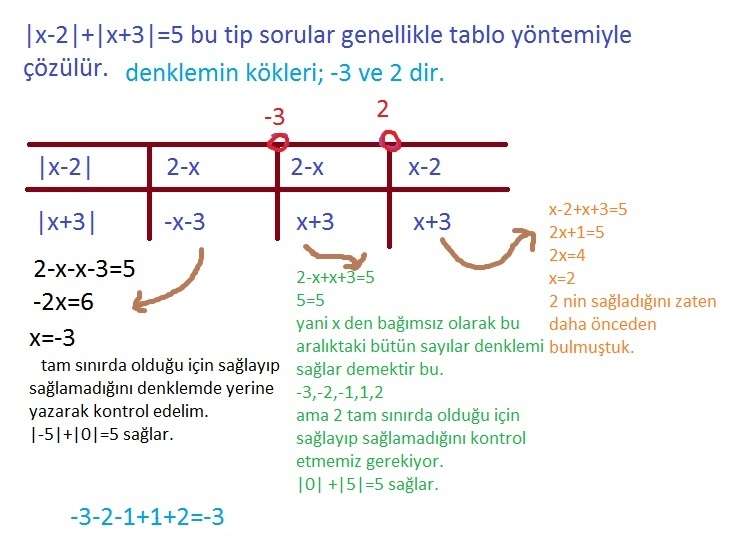
1)|2x-4|+|2x+6|=10 denklemini sağlayan x tamsayılarının toplamı kaçtır?c:-3
2)|x-5/x+2|>0 eşitsizliğini sağlayan x değerlerinin toplamı kaçtır?c:-3
3)|x²+2x-8|-|x-2|=0 ddenklemini sağlayan x reel sayılarının toplamı kaçtır?c:-6
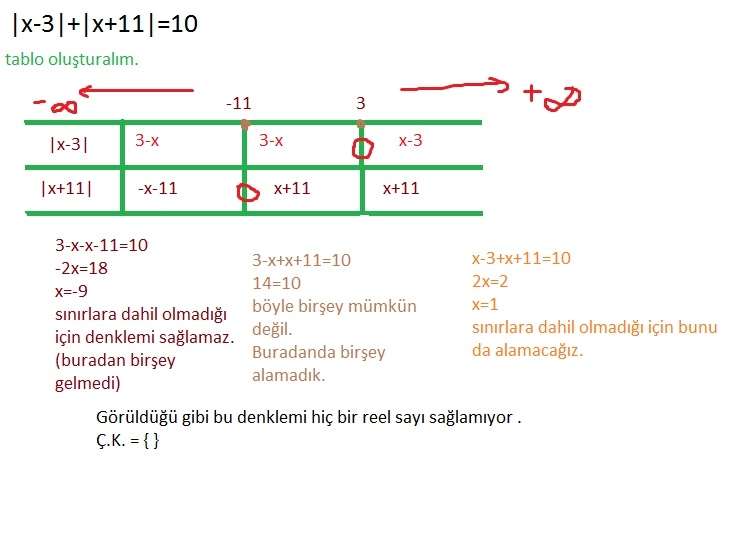
4)|x-3|+|x+11|=10 denkleminin çözüm kümesi nedir?c:{ }boş küme
5)|-2/x-3|≥1/2 eşitsizliğini sağlayan kaç tane x tamsayısı vardır?c:8
2)|x-5/x+2|>0 eşitsizliğini sağlayan x değerlerinin toplamı kaçtır?c:-3
3)|x²+2x-8|-|x-2|=0 ddenklemini sağlayan x reel sayılarının toplamı kaçtır?c:-6
4)|x-3|+|x+11|=10 denkleminin çözüm kümesi nedir?c:{ }boş küme
5)|-2/x-3|≥1/2 eşitsizliğini sağlayan kaç tane x tamsayısı vardır?c:8
C-1)

C-4)

C-3)
|(x+4).(x-2)|-|x-2|=0
|x+4|.|x-2|=|x-2|
x-2≠0 şartı altında çözüm yapalım;
x+4=4, x+4=-1
x=-3, x=-5
Bundan ayrı olarak denklemi 2 de sağlıyor.
Toplamları;
2-3-5=-6
|(x+4).(x-2)|-|x-2|=0
|x+4|.|x-2|=|x-2|
x-2≠0 şartı altında çözüm yapalım;
x+4=4, x+4=-1
x=-3, x=-5
Bundan ayrı olarak denklemi 2 de sağlıyor.
Toplamları;
2-3-5=-6
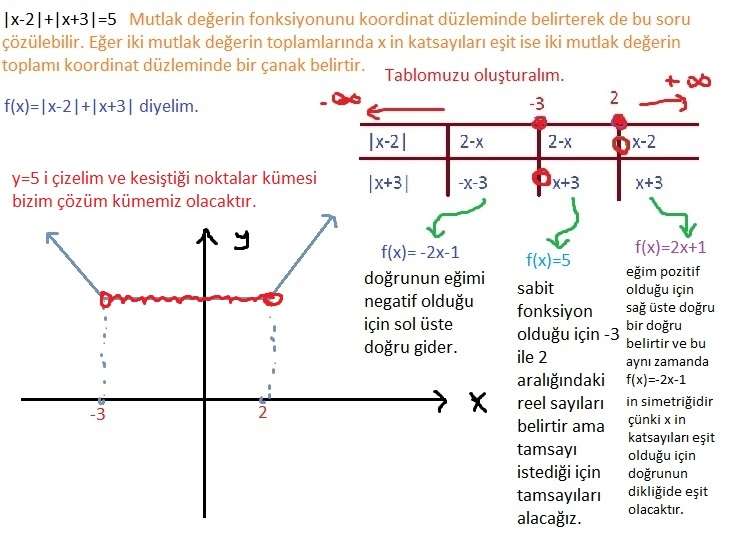
1. SORU 2. YOL
Eğer iki mutlak değerin toplamında x in katsayıları eşitse fonksiyonu koordinat düzleminde bir çanak belirtir. Bu yöntemle bu tip soruları daha kısa zamanda çözebilirsiniz.

Eğer iki mutlak değerin toplamında x in katsayıları eşitse fonksiyonu koordinat düzleminde bir çanak belirtir. Bu yöntemle bu tip soruları daha kısa zamanda çözebilirsiniz.
C-5)
|-2/x-3|≥1/2, soruyu yanlış yazdın heralde doğrusu |-2/(x-3)|≥1/2 olacaktı.
Eğer öyleyse çözüm yapıyorum.
|-2/(x-3)|≥1/2
2/|x-3|≥1/2
denklemin çarpmaya göre tersini alırsak yön değiştirecektir.
|x-3|/2 ≤2
|x-3| ≤ 4
-4 ≤ x-3 ≤ 4
-1 ≤ x ≤ 7, burada 9 değer var ama 3 denklemi tanımsız yaptığından onu alamayız dolayısıyla 8 değer vardır bu şartı sağlayan.
|-2/x-3|≥1/2, soruyu yanlış yazdın heralde doğrusu |-2/(x-3)|≥1/2 olacaktı.
Eğer öyleyse çözüm yapıyorum.
|-2/(x-3)|≥1/2
2/|x-3|≥1/2
denklemin çarpmaya göre tersini alırsak yön değiştirecektir.
|x-3|/2 ≤2
|x-3| ≤ 4
-4 ≤ x-3 ≤ 4
-1 ≤ x ≤ 7, burada 9 değer var ama 3 denklemi tanımsız yaptığından onu alamayız dolayısıyla 8 değer vardır bu şartı sağlayan.
Teşekkür ederim.Çok sağol 
Diğer çözümlü sorular alttadır.
