kümeler

SORU1: s(A−B)=4.s(B−A) ve
s(A)+s(B)=13 olmak üzere
A∩B kümesinin eleman sayısı aşağıdakilerden hangisine eşittir?
A) 5 B)4 C)3 D)2 E)1

Soru2: A∩B≠Ø, s(A)=2x+1, s(B)=3x−7 ve s(A∩B)=5−x olmak üzere, s(A∪B)nin alabileceği en büyük ve en küçük değerin toplamı kaçtır?
A)14 B)20 C)26 D)32 E)38

SORU3: { x|1≤x≤500, x∈Z} olmak üzere, A kümesinin 3 ile bölünebilen ve 7 ile bölünemeyen kaç tane elemanı vardır?
A)143 B)140 C)95 D)62 E)48

SORU4: Akümesinin elemanlarının %85i B kümesinin elemanı değildir. B kümesinin elemanlarının %10 u da, A kümesinin elemanı değildir. S(A∪B)=305 ise s(A-B) kaçtır?

Soru5: A ve B boş olmayan iki kümedir
A≠B, B⊂A ve s(A∩B=2s(A-B)+5 olduğuna göre, A∩B nin eleman sayısı en az kaçtır?

cevap 1

A=x ve B=y dersek x-y=4(x-y) ==> 3x=3y ve x=y olur burdan A∩B=1 olur yani E şıkkı

1.soruyu yanlış yazmışım ama siz doğru bir cevap vermişsiniz. Yine de teşekkür ederim

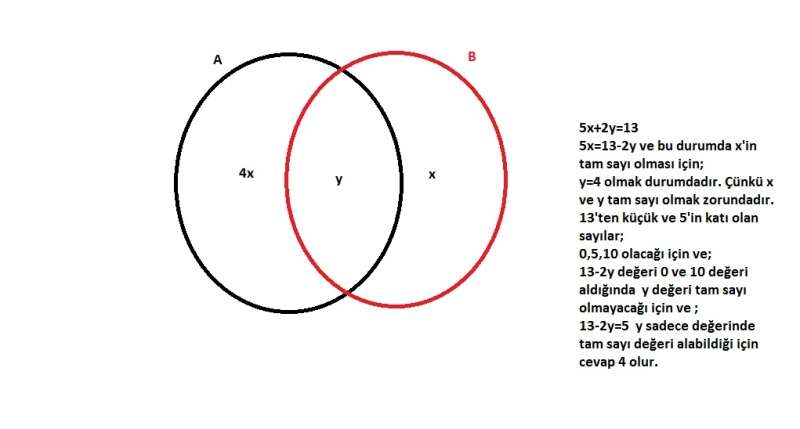
Bu durumda cevabı şu şekilde açıklayabiliriz;



Arkadaşımıza yanlış yaptı diyemeyiz bu durumda

Evet yanlış yazmışım şimdi düzelttim

2)
s(A)=2x+1, s(B)=3x−7 ve
s(A∩B)=5−x ve A∩B≠Ø ise x<5 olmak zorundadır.
x=4 için istenilen değer en büyük değerini alır;
x=4 için; s(A)=9, s(B)=5, s(A∩B)=1 bu durumda: s(AuB)=9+5-1=13
A∩B≠Ø ise s(B)≠0 olur bu durumda;
3x-7>0 ve 3x>7 olur. Sonuç olarak x'in alabileceği en küçük değerin 3 olduğunu görüyoruz.
x=3 için istenilen değer en küçük değerini alır;
x=3 için; s(A)=7, s(B)=2, s(A∩B)=2 bu durumda: s(AuB)=7+2-2=7
s(AuB) değerinin alabileceği en küçük değer ile en büyük değerin toplamı;
13+7=20

3)
3 ile bölünüp 7 ile bölünemeyen elemanları bulmak için öncelikle 3 ile bölünebilen elemanları buluruz.
Sonra hem 3 ile hem 7 ile bölünen (Yani 21 ile bölünebilen) elemanları buluruz.
3 ile bölünebilen elemanlardan 21 ile bölünebilen elemanları çıkarıp sonucu buluruz.
3 ile bölünebilen x sayısı;
500/3=166
3/3=1 ise buradan 166 tane x elemanı olduğunu görüyoruz.
21 ile bölünebilen x sayısı;
500/21=23
21/21=1 ise buradan da 23 tane x elemanı olduğunu görüyoruz.
166-23=143

4)
s(A)=100k ise;
s(A/B)=85k
s(AnB)=15k
s(B)=100m ise;
90m=15k
6m=k
m=t ve k=6t olsun;
s(AUB)=100t+600t-90t=305
610t=305
t=1/2
s(A/B)=85k=85.6t=85.6.1/2
=255

5)
s(A-B)=x ise;
s(A∩B)=2x+5
A≠B, B⊂A ise x≠0
Bu durumda x en küçük 1 değerini alır.
x=1 ise;
2x+5=7

Evet benim hatam. Çözümleriniz için teşekkür ederiiiiim.