matsevdasi72 01:40 09 Kas 2012 #1
Arkadaşlar bunu bulamadım.Bulan olursa nasıl bulduğunu yazarsa sevinirim...
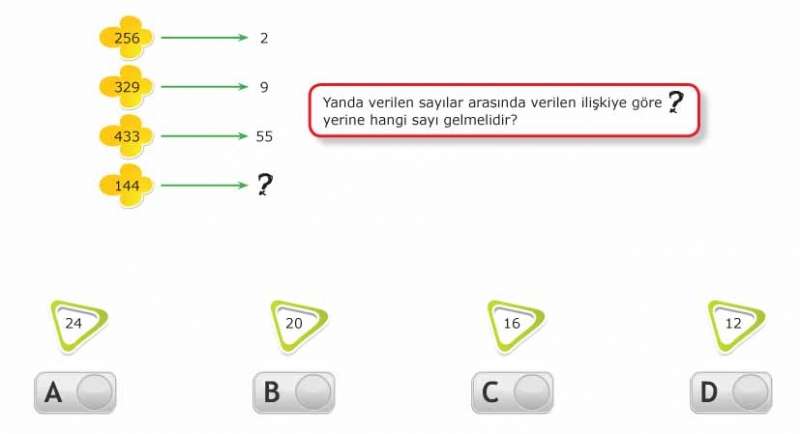
256-------> 2
329-------> 9
433-------> 55
144-------> ?
soru işareti yerine hangi sayı gelecek
12-16-20-24----şıklar...
256-------> 2
329-------> 9
433-------> 55
144-------> ?
soru işareti yerine hangi sayı gelecek
12-16-20-24----şıklar...
matsevdasi72 22:52 10 Kas 2012 #2
Evet arkadaşlar cevabı bulabilen yok mu?
gereksizyorumcu 23:23 10 Kas 2012 #3
şimdi cevaba 5 desem hangi kurala göre yanlış olduğunu söyleyecekler?
neyse ben 15 için basit bi kural buldum
sayı abc ise |ab-bc| şeklinde bir kural olabiliyor, tabi her zamanki gibi yazmadan geçmeyelim soru işareti yerine istediğiniz şey gelebilir, yani verilen her seçenek için hatta doğum yılınız için bile bi kural üretilebilir.
neyse ben 15 için basit bi kural buldum
sayı abc ise |ab-bc| şeklinde bir kural olabiliyor, tabi her zamanki gibi yazmadan geçmeyelim soru işareti yerine istediğiniz şey gelebilir, yani verilen her seçenek için hatta doğum yılınız için bile bi kural üretilebilir.
matsevdasi72 13:10 11 Kas 2012 #4 şimdi cevaba 5 desem hangi kurala göre yanlış olduğunu söyleyecekler?
neyse ben 15 için basit bi kural buldum
sayı abc ise |ab-bc| şeklinde bir kural olabiliyor, tabi her zamanki gibi yazmadan geçmeyelim soru işareti yerine istediğiniz şey gelebilir, yani verilen her seçenek için hatta doğum yılınız için bile bi kural üretilebilir.
neyse ben 15 için basit bi kural buldum
sayı abc ise |ab-bc| şeklinde bir kural olabiliyor, tabi her zamanki gibi yazmadan geçmeyelim soru işareti yerine istediğiniz şey gelebilir, yani verilen her seçenek için hatta doğum yılınız için bile bi kural üretilebilir.
Fatal zking 17:18 11 Kas 2012 #5
bu sorunun cebı anahtarı varmı ?
gereksizyorumcu 18:05 11 Kas 2012 #6 Mantığınız doğru ama cevap 12 diyor...
"aklımdan bi sayı tuttum, bu sayı nedir?
a)1 b)2 c)3 d)4 e) hiçbiri "
sonuçta bu yazdığım soruda da soru metninde belirtilmeyen sadece soruyu üretenin aklındaki bişeyi bulmaya çalışıyorsunuz.
Fatal zking 18:15 11 Kas 2012 #7
Yani sorunun cevabı yok
@gereksizyorumcu sorunun birden çok cevabı olduğundan bahsediyor.
Fatal zking 18:23 11 Kas 2012 #9
yani 1 den fazla cevap ?
n² örüntüsü var diyelim.
1,4,9,16,25,... diye giden. 25 ten 36 geleceği düşünürken ben istediğim sayıyı getirebilirim özel bir kural bularak örneğin.
an=(n-1).(n-2).(n-3).(n-4).(n-5)+n² kuralı ile.
n=1 için a1=1
n=2 için a2=4
n=3 için a3=9
n=4 için a4=16
n=5 için a5=25
n=6 için a6= 5.4.3.2.1+6²=120+36=276 bulabilirim.
İstersem an=n.(n-1).(n-2).(n-3).(n-4).(n-5).+n²
kuralı ile ilk beş terimi aynı bu sefer 6. terimi a6=6!+6²=720+36=756 bulabilirim örneğin.
Yani, hocamın verdiği örüntüye uygun bir kaç kural bulunarak sorulan yere gelebilecek birden fazla sayı bulunabilir.
Eeeee, bunlar bunu bilmiyorlar mı? Biliyorlardır muhtemelen. Burada handikap sayı örüntüleri kavramının matematikçiler tarafından iyi tanımlanmamış olmasıdır.
1,4,9,16,25,... diye giden. 25 ten 36 geleceği düşünürken ben istediğim sayıyı getirebilirim özel bir kural bularak örneğin.
an=(n-1).(n-2).(n-3).(n-4).(n-5)+n² kuralı ile.
n=1 için a1=1
n=2 için a2=4
n=3 için a3=9
n=4 için a4=16
n=5 için a5=25
n=6 için a6= 5.4.3.2.1+6²=120+36=276 bulabilirim.
İstersem an=n.(n-1).(n-2).(n-3).(n-4).(n-5).+n²
kuralı ile ilk beş terimi aynı bu sefer 6. terimi a6=6!+6²=720+36=756 bulabilirim örneğin.
Yani, hocamın verdiği örüntüye uygun bir kaç kural bulunarak sorulan yere gelebilecek birden fazla sayı bulunabilir.
Eeeee, bunlar bunu bilmiyorlar mı? Biliyorlardır muhtemelen. Burada handikap sayı örüntüleri kavramının matematikçiler tarafından iyi tanımlanmamış olmasıdır.