C-1) prizmayı şekildeki gibi kenarlara paralel olacak şekilde bölersek
sağda kalan dikdörtgenler prizmasının alanın yarısı sarı üçgen prizmadır. Kısaca şöylemek gerekirse bu yüzden hacmi de yarısıdır.
solda kalan dikdörtgenler prizmasının alanın yarısı sarı üçgen prizmadır.Kısaca şöylemek gerekirse bu yüzden hacmi de yarısıdır.
O zaman tüm dikdörtgenler prizmasının hacminin yarısı istenen tüm sarı bölge altındaki üçgen prizmanın hacmidir.
Yani 120:2=60 dır cevap
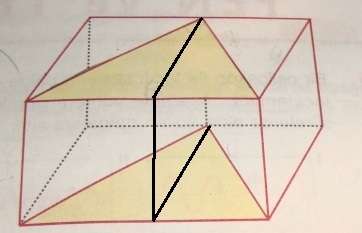
sağda kalan dikdörtgenler prizmasının alanın yarısı sarı üçgen prizmadır. Kısaca şöylemek gerekirse bu yüzden hacmi de yarısıdır.
solda kalan dikdörtgenler prizmasının alanın yarısı sarı üçgen prizmadır.Kısaca şöylemek gerekirse bu yüzden hacmi de yarısıdır.
O zaman tüm dikdörtgenler prizmasının hacminin yarısı istenen tüm sarı bölge altındaki üçgen prizmanın hacmidir.
Yani 120:2=60 dır cevap
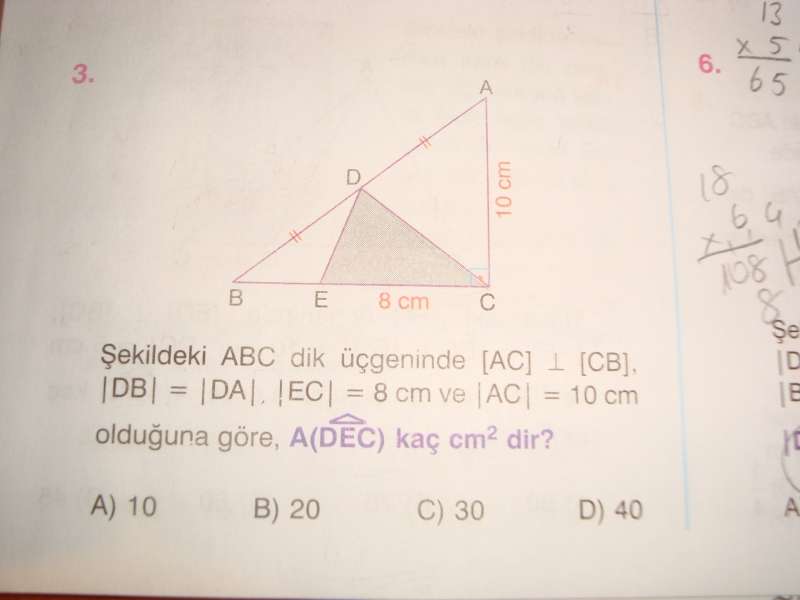
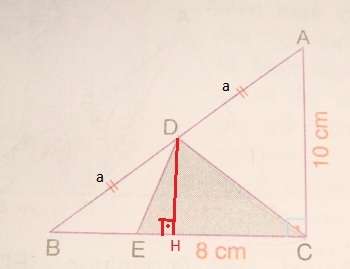
C-3) [DH] dikliğini çizebiliriz.
[DH] paralel [AC] olacaktır.
İki diklik ve diğer diğer açılarından DHB üçgeni ile ACB üçgeni benzer olacaktır.
Bu benzerlikten |BD| / |BA| = |DH| / |AC| dir. Değerlerini yerine yazarsak
a / 2a = |DH| / 10 ise |DH|=5 bulunur.
İstenen üçgenin alanı 5.8/2=20 dir.
[DH] paralel [AC] olacaktır.
İki diklik ve diğer diğer açılarından DHB üçgeni ile ACB üçgeni benzer olacaktır.
Bu benzerlikten |BD| / |BA| = |DH| / |AC| dir. Değerlerini yerine yazarsak
a / 2a = |DH| / 10 ise |DH|=5 bulunur.
İstenen üçgenin alanı 5.8/2=20 dir.
C-4) Bu sorunun kısa bir yolu var . Öklid Bağıntılarını bir yerden duymuşsan çok kolay yapılır. ancak 8. sınıf konusu değil öklid bağıntıları.
Bilmiyorsan bir çok denklemi çözmen gerekiyor. Ben kısa olması için Öklid formülün (Öklid Bağıntısı Bağıntıları Formülü Formülleri)den analatacağım.
Şöyle bir öklid bağıntısı vardır.
bu formülde verilenleri yerine yazarsak
payda eşitlenir ve çıkarma yapılırsa
her iki taraf ters çevirilirse
her iki tarafın karekökü alınırsa
|AB|=12.13/5 olacaktır.
|AB|=156/5
Bilmiyorsan bir çok denklemi çözmen gerekiyor. Ben kısa olması için Öklid formülün (Öklid Bağıntısı Bağıntıları Formülü Formülleri)den analatacağım.
Şöyle bir öklid bağıntısı vardır.
1
|AC|²
+
1
|AB|²
=
1
|AH|²
bu formülde verilenleri yerine yazarsak
1
13²
+
1
|AB|²
=
1
12²
1
|AB|²
=
1
12²
−
1
13²
payda eşitlenir ve çıkarma yapılırsa
1
|AB|²
=
13²−12²
12².13²
1
|AB|²
=
5²
12².13²
her iki taraf ters çevirilirse
|AB|²=
12².13²
5²
her iki tarafın karekökü alınırsa
|AB|=12.13/5 olacaktır.
|AB|=156/5
hepinize çok teşekkür ederim...
suzan kahraman 19:04 23 May 2012 #7
peki bunu nerden anlıycaz her şekilde bu geçerli mi veya hangi şekillerde geçerlidr?
suzan kahraman 19:14 23 May 2012 #8
hocam öklid bilmiyoruz dediğiniz gibi acaba denklemle nasıl çözeriz birde şu benzerlikleri görmenn basit bir yolu var mı?
Diğer çözümlü sorular alttadır.