1- 2004 ÖO sorusu
Bir küre içine yerleştirilen silindirin yarıçapı 4 cm. ve hacmi 96∏ cm3'tür. Bu kürenin yarıçapı en az kaç cm olur?
a) 10 b) 8 c)6 d) 5
2-
3-
4- 2010 SBS Sorusu

5- 2009 sbs sorusu

Cevaplar için şimdiden çok teşekkürler
Bir küre içine yerleştirilen silindirin yarıçapı 4 cm. ve hacmi 96∏ cm3'tür. Bu kürenin yarıçapı en az kaç cm olur?
a) 10 b) 8 c)6 d) 5
2-

3-

4- 2010 SBS Sorusu
5- 2009 sbs sorusu

Cevaplar için şimdiden çok teşekkürler
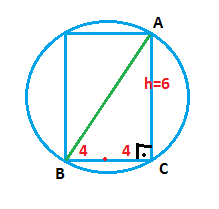
C-1) silindirin hacmi: pi.4².h=96.pi => h=6 dır.

Silindirin taban ve tavan daireleri üzerinde alınacak iki nokta şekildeki gibi olacaktır (A ve B noktaları). Bu uzunluk en kısa A;B ve C noktaları aynı düzlem üzerinde olduğundan en küçük olacaktır.
Bu 3 nokta aynı düzlem üzerinde olduğunda şekildeki gibi bir dik üçgen oluşur.Pisagordan |AB|=10 ve kürenin yarıçapı bu uzunluğun yarısı olabilir en az. r=5 olabilir en küçük yani. cevap d şıkkı. (not: bu soru 8. sınıf için zor bir sorudur)
C-2) Burada 3 farklı yüzey alanı bulunup toplanacak.
1. dış silindirin yanal alanı
2. iç silindirin yanala alanı
3. üstte ve altta daireler arası kalan alan.
Dış silindirin yanal alanı; silindirin açık şekli düşünüldüğünde Bir dikdörtgen alanıdır.
Boyu, 2.pi.10 ve eni (silindiirn yüksekliğidir) 20 cm yani alan : 2.3.10.20=1200 cm²
İç silindirin yanal alanı; Yine dikdörtgen düşünülecek. 2.pi.9 ve eni 20 cm alan: 2.3.9.20=1080 cm²
Üstte ve altta daireler arası kalan alan; üsttekinin alanı, büyük daire alanı eksi küçük dairenin alanı: pi.10²−pi.9²=57cm² ve bu alandan alttada vardır. 57.2=114 cm²
Tüm istenen alan: 1200+1080+114=2394 cevap B şıkkı.
Silindirin taban ve tavan daireleri üzerinde alınacak iki nokta şekildeki gibi olacaktır (A ve B noktaları). Bu uzunluk en kısa A;B ve C noktaları aynı düzlem üzerinde olduğundan en küçük olacaktır.
Bu 3 nokta aynı düzlem üzerinde olduğunda şekildeki gibi bir dik üçgen oluşur.Pisagordan |AB|=10 ve kürenin yarıçapı bu uzunluğun yarısı olabilir en az. r=5 olabilir en küçük yani. cevap d şıkkı. (not: bu soru 8. sınıf için zor bir sorudur)
C-2) Burada 3 farklı yüzey alanı bulunup toplanacak.
1. dış silindirin yanal alanı
2. iç silindirin yanala alanı
3. üstte ve altta daireler arası kalan alan.
Dış silindirin yanal alanı; silindirin açık şekli düşünüldüğünde Bir dikdörtgen alanıdır.
Boyu, 2.pi.10 ve eni (silindiirn yüksekliğidir) 20 cm yani alan : 2.3.10.20=1200 cm²
İç silindirin yanal alanı; Yine dikdörtgen düşünülecek. 2.pi.9 ve eni 20 cm alan: 2.3.9.20=1080 cm²
Üstte ve altta daireler arası kalan alan; üsttekinin alanı, büyük daire alanı eksi küçük dairenin alanı: pi.10²−pi.9²=57cm² ve bu alandan alttada vardır. 57.2=114 cm²
Tüm istenen alan: 1200+1080+114=2394 cevap B şıkkı.
C-3) kesilen 120 derece silindirin açık şeklindeki boyundan 1/3 oranında azalmasına sebep olur. Ayrıca kesilen bölgede 2 tane eş dikdörtgen yüzeyinin alanı hesaba katılmalıdır.
Açık silindirin boyu: 2.pi.10-(2.pi.10/3)=40 cm dir ve eni (h) 20 cm dir. Alanı: 40.20=800 cm² dir.
Kesinlen bölgedeki dikdörtgenlerin toplam alanı: 2.r.h=2.10.20=400 cm² dir. Toplam yüzey alanı: 800+400=1200cm² cevap B şıkkıdır.
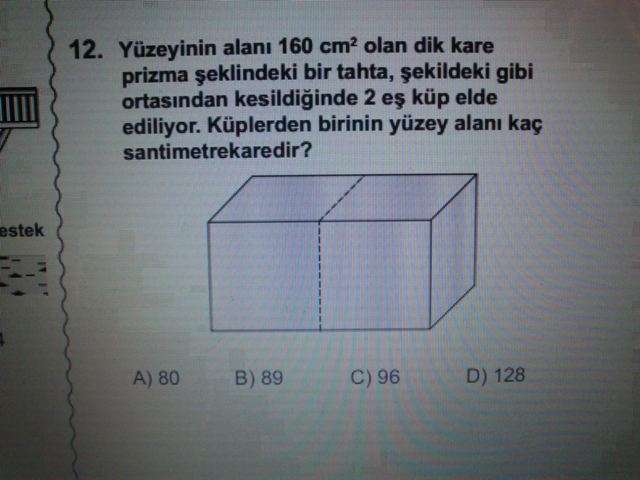
C-4) bu şeklin yüzey alanı 10 tane eş kareden oluşuyor. O zaman bir tanesinin alanı 160:10=16 cm² dir. Bölündüğünde bir küpte bu karelerden 6 tane olacaktır. 16.6=96 cm² cevap şıkkıdır.
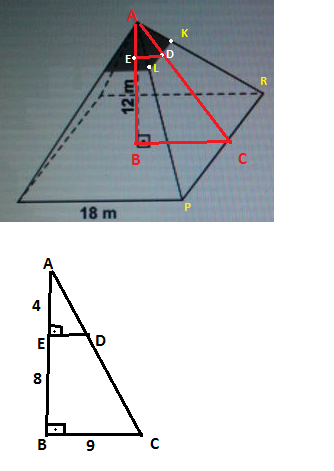
C-5) istenen şeklin yan yüz alanlarının bulunabilmesi için tepeden gelen yükseklik ile yan yüzler arasında oluşacak alttaki üçgeni görebilmemiz gerekmektedir.

Pisagordan |AC|=15cm ve benzerlik uygulanırsa |AD|=5 cm bulunur. Aynı benzerlik LK ile PR arasında vardır ve LK, PR nin 1/3 dür. |LK|=6 cm dir. AL ile LK diktir ve Bu üçgenin üyksekliği 6.5/2=15 cm² dir ve bu üçgenden 4 tane vardır her tarafında. 4.15=60 cm² cevap b şıkkıdır. (bu soru lys ayarında bir sorudur)
Açık silindirin boyu: 2.pi.10-(2.pi.10/3)=40 cm dir ve eni (h) 20 cm dir. Alanı: 40.20=800 cm² dir.
Kesinlen bölgedeki dikdörtgenlerin toplam alanı: 2.r.h=2.10.20=400 cm² dir. Toplam yüzey alanı: 800+400=1200cm² cevap B şıkkıdır.
C-4) bu şeklin yüzey alanı 10 tane eş kareden oluşuyor. O zaman bir tanesinin alanı 160:10=16 cm² dir. Bölündüğünde bir küpte bu karelerden 6 tane olacaktır. 16.6=96 cm² cevap şıkkıdır.
C-5) istenen şeklin yan yüz alanlarının bulunabilmesi için tepeden gelen yükseklik ile yan yüzler arasında oluşacak alttaki üçgeni görebilmemiz gerekmektedir.
Pisagordan |AC|=15cm ve benzerlik uygulanırsa |AD|=5 cm bulunur. Aynı benzerlik LK ile PR arasında vardır ve LK, PR nin 1/3 dür. |LK|=6 cm dir. AL ile LK diktir ve Bu üçgenin üyksekliği 6.5/2=15 cm² dir ve bu üçgenden 4 tane vardır her tarafında. 4.15=60 cm² cevap b şıkkıdır. (bu soru lys ayarında bir sorudur)
Çok teşekkür ederim... Açıklamaları için ayrıca teşekkür ederim 
Diğer çözümlü sorular alttadır.
.8. sınıf Geometri Soruları ve Çözümleri .8. sınıf Geometrik Cisimler Soruları .8. sınıf Küp Soruları Çözümleri .8. sınıf Piramit Soruları Çözümleri .8. sınıf Prizma Soruları Çözümleri
Tüm Etiketler
Tüm Etiketler
