limit

çözerseniz sevinirim şimdiden teşekkürler

Cevapları da yazabilir misin ?
TAKİP

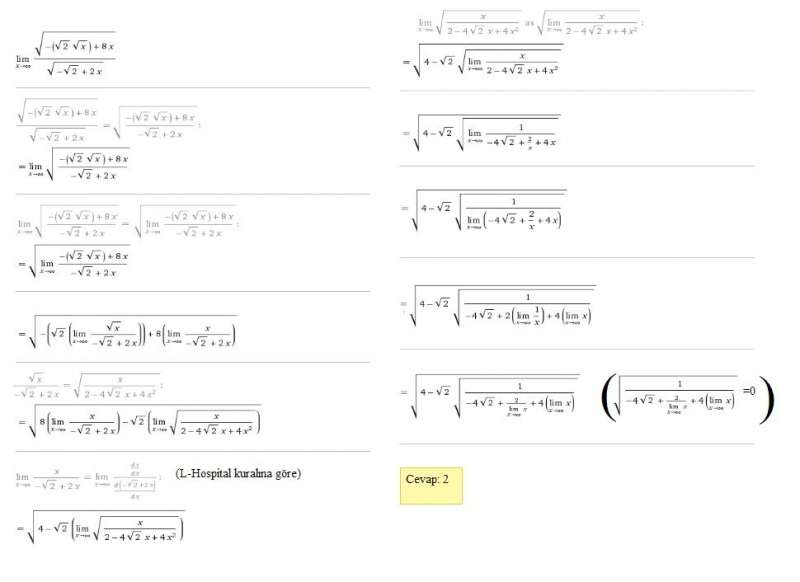
1) İlk olarak sorunun bilimsel ve uzun çözümünü yapalım sonra asıl çözüm yöntemiyle çözelim;




2. Yol;

∞/∞ belirsizliğinde pay ve paydadaki en büyük değişkenleri alarak işlem yapılır.Yani ifade √8x/√2x =2 olarak düşünülebilir.

teşekkürler

1 b
2 d
3 e
4 c
şimdiden teşekkürler

2)1^∞ belirsizliğinde ifadeyi (1+f(x))^g(x) haline getirerek;

(1+[(2n+1)/(3n²+1)])^4n²/(2n+1) ifadede;

e^{lim_(n->∞) g(x).f(x)} i kullanırsak;

e^{lim_(n->∞) [4n²/(2n+1)].[(2n+1)/(3n²+1)]}= e^4/3 olacaktır.

3) ∞.0 belirsizliğinde ifade ∞/∞ veya 0/0 belirsizliğine dönüştürülerek işlem yapılır;

Bu durumda ifade;

lim_(x->∞) [sin(2/x)]/(1/(3x-1))] şeklinde yazılırsa 0/0 belirsizliğine dönüşmüş olur. Burada direk sinüslü terim sinüs kaldırılarak işlem yapılacağından;

(2/x)/(1/(3x-1))= ((6x-2)/x) için ∞/∞ a göre işlem yaparak en büyük terimlerin katsayılarını oranlarsak sonuç 6/1=6 olacaktır.

4)0/0 belirsizliği için işlem yapacağımızdan tanjantlı ifadelerin yalnız iç kısımlarını alırsak ve x ile oranlama yaparsak;

2+4+6+8+....+100 toplamını elde ederiz. İfadeyi 2(1+2+3+4+....+50)şeklinde yazarak;

[son terim.(son terim+1)/2] toplam formülünden 2.(50.51/2)=2550 sonucuna ulaşırız.

teşekkür ederim

Enes,bunlar ne böyle?
Yerinde olmadan üşendim vallahi,çok açıklayıcı olmuş yüreğine,ellerine sağlık.