1)f(x)=||2-x|-4| ve g(x)=1 fonksiyonlarının grafiklerinin kesim noktaları arasındaki uzaklık en fazla kaç birimdir?(10)
2)|x+y|=2 bağıntısının grafiği ile eksenler arasında kalan üçgensel bölgelerin alanları toplamı kaçtır?(4)
3)f(x)=|x+4|-|x-1| fonksiyonunun görüntü kümesinde kaç tam sayı vardır?(11)
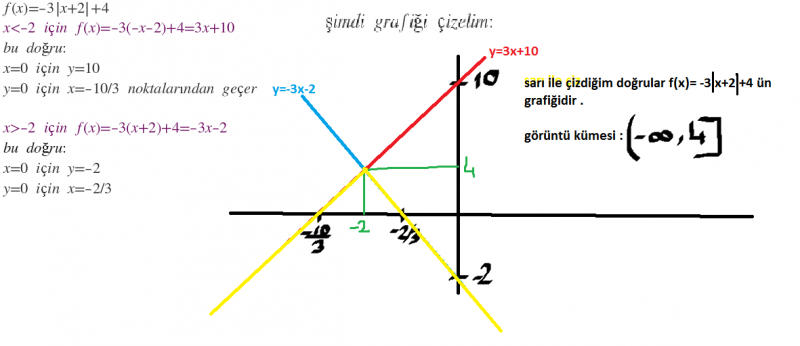
4)f:R'den R'ye olmak üzere f(x)=-3|x+2|+4 fonksiyonunun görüntü kümesi nedir?(-∞,4]
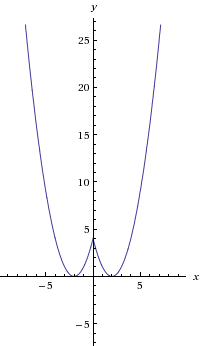
5)f(x)=x²-4x+4
g(x)=f(|x|)
h(x)=2m-4
olmak üzere g(x) ve h(x) fonksiyonlarının grafikleri 3 farklı noktada kesişiyorsa m kaçtır?(3)