1) 
(C)
2)
[2,6]
3)
(-4,8)
4)6 kişi üçer kişilik 2 gruba ayrılacaktır.Bu işlem kaç farklı şekilde yapılabilir?(10)
5)ahmet 10 farklı kalemden 3 ünü seçip üç kardeşine 1 er tane hediye edecektir.Bu işlem kaç farklı biçimde gerçekleştirilebilir(720)

(C)
2)
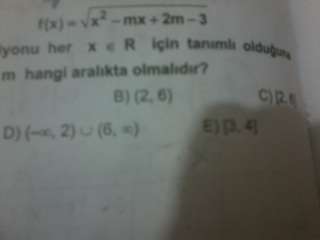
[2,6]
3)

(-4,8)
4)6 kişi üçer kişilik 2 gruba ayrılacaktır.Bu işlem kaç farklı şekilde yapılabilir?(10)
5)ahmet 10 farklı kalemden 3 ünü seçip üç kardeşine 1 er tane hediye edecektir.Bu işlem kaç farklı biçimde gerçekleştirilebilir(720)
4.
6 kişiden ilk üçünü seçelim C(6,3)=20
sayımlarımız simetrik olacaktır ha ab ha ba , 20/2 = 10
5.
C(10,3)=10.9.8/3.2 => 120 durum.
10 kalemden 3ünü seçtik şimdi bu 3 kalemi 3 kardeş arasında dağıtacağız (bir nevi dizilim) bu da 3!=6 şekilde olur.
6.120=720
6 kişiden ilk üçünü seçelim C(6,3)=20
sayımlarımız simetrik olacaktır ha ab ha ba , 20/2 = 10
5.
C(10,3)=10.9.8/3.2 => 120 durum.
10 kalemden 3ünü seçtik şimdi bu 3 kalemi 3 kardeş arasında dağıtacağız (bir nevi dizilim) bu da 3!=6 şekilde olur.
6.120=720
1) Soruda ilk olarak (fog)(x)=3|x+1|-3x+1 olarak yazalım. Sonra yeni fonksiyonumuzu parçalı hale getirelim:

Bu durumda elimizde iki farklı fonksiyon bulunmakta;
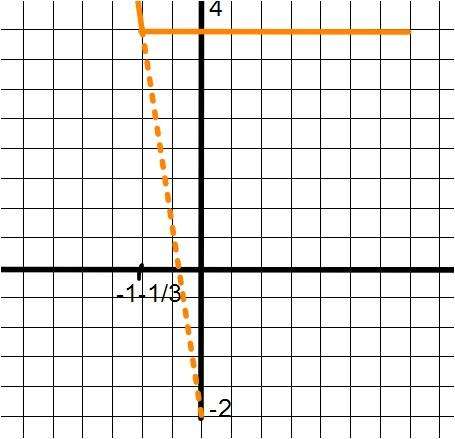
f(x)=4 ve f(x)=-6x-2 bu iki fonksiyonun grafiği bizim için (fog)(x) in grafiği olacağından;

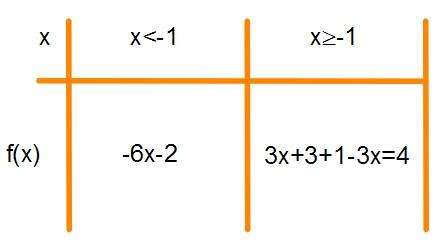
Bu durumda elimizde iki farklı fonksiyon bulunmakta;
f(x)=4 ve f(x)=-6x-2 bu iki fonksiyonun grafiği bizim için (fog)(x) in grafiği olacağından;
2)Kökün içi bir parabol belirttiğine göre bu parablün en küçük değeri tepe noktasının y değeri olacağından (4ac-b²)/4a den
8m-12-m²≥0 buradan m²-8m+12≤0 o halde eşitsizlik çözümü yapılacak olursa m∈[2,6] olarak bulunur.
8m-12-m²≥0 buradan m²-8m+12≤0 o halde eşitsizlik çözümü yapılacak olursa m∈[2,6] olarak bulunur.
3) Soruda verilen fonksiyonun R de tanımlı olabilmesi için paydanın hiç bir şekilde 0 a eşit olmaması lazım. Bunun için denklemin gerçek kökünün olmaması lazım. Bu durumda paydanın diskriminantı 0 dan küçük olmalıdır.
m²-4m-32<0 ise (m-8)(m+4)<0 dan eşitsizlik çözümü yapılır ve sonuç; m∈(-4,8) açık aralığı bulunur.
Eşitsizlik çözümlerinde sorun yaşarsanız yardımcı olabilirim.
m²-4m-32<0 ise (m-8)(m+4)<0 dan eşitsizlik çözümü yapılır ve sonuç; m∈(-4,8) açık aralığı bulunur.
Eşitsizlik çözümlerinde sorun yaşarsanız yardımcı olabilirim.
Çoook teşekkür ederim evet eşitsizlik sıkıntı biraz yardımcı olursanız çok sevinirim
evet eşitsizlik sıkıntı biraz yardımcı olursanız çok sevinirim
2. soru için m²-8m+12≤0 eşitsizliği sanki sıfıra eşitmiş gibi denlem çözümü yapılarak eşitsizlik grafiğimizin dönüm noktalarını bulabiliriz. m²-8m+12=0 ise (m-2)(m-6)=0 dan denklemin kökleri 2 ve 6 olarak bulunur.
Bu durumda eşitsizlik grafiğimiz;

şeklindedir.
Bizim için sıfırdan küçük ve sıfıra eşit değerleri sağlayacak aralık gerektiğinden m∈[2,6] olarak bulunur.
Bu durumda eşitsizlik grafiğimiz;
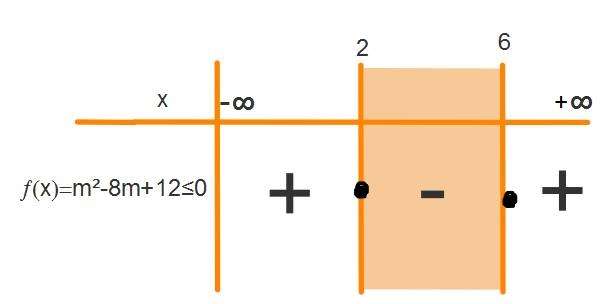
şeklindedir.
Bizim için sıfırdan küçük ve sıfıra eşit değerleri sağlayacak aralık gerektiğinden m∈[2,6] olarak bulunur.
3. soru için; m²-4m-32<0 eşitsizliği sanki sıfıra eşitmiş gibi denlem çözümü yapılarak eşitsizlik grafiğimizin dönüm noktalarını bulabiliriz.
(m-8)(m+4)=0 ise denklemin kökleri -4 ve 8 olarak bulunur.
Bu durumda eşitsizlik grafiğimiz;

şeklinde olur.
Bizim için sıfırdan küçük değerleri sağlayacak aralık gerektiğinden sonuç m∈(-4,8) açık aralığı bulunur.
(m-8)(m+4)=0 ise denklemin kökleri -4 ve 8 olarak bulunur.
Bu durumda eşitsizlik grafiğimiz;
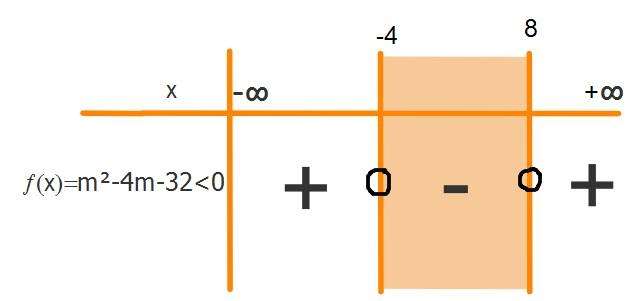
şeklinde olur.
Bizim için sıfırdan küçük değerleri sağlayacak aralık gerektiğinden sonuç m∈(-4,8) açık aralığı bulunur.
Teşekkür ederim
