

4) f(x)= |50-2x²|-|x²-25| fonksiyonunun parçalı fonksiyon olarak ifadesi aşağıdakilerden hangisidir?
A) 75-3x², -5<x<5
3x²-75, x≤-5 veya 5≤x
B) x²-25, -5<x<5
25-x², x≤-5 veya 5≤x
C) 25-x², -5<x<5
x²-25, x≤-5 veya 5≤x
D) 5-x, x≤-5
x-5, -5<x
E) x-5, x<5
5-x, 5≤x
5)IR den IR ye tanımlı f(x) fonksiyonu çift fonksiyondur.
f(x)+ x. f(-x) + x². f(-x) = x⁴+x³+2x²+x+1 olduğuna göre f(-2x) in eşiti aşağıdakilerden hangisidir?
A) x²−x/2
B) 2x²-x
C) 4x²+1
D) 6x²-3x
E) 8x²-4x
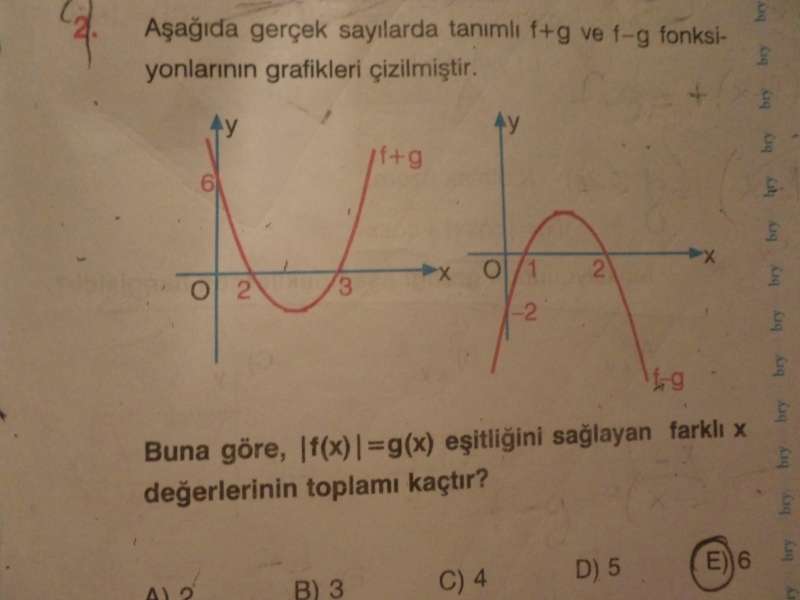
f+g = a (x-2)(x-3)
x=0 için y=6 olacağından 6a=6 a=1 olur yani f+g = (x-2)(x-3) = x²-5x+6 ...(1)
f-g = a₂(x-1)(x+2)
x=0 için y=-2 olacağından 2a₂=-2 a²=-1 olur yani f-g =-1(x-1)(x-2)=-x²+3x-2 ...(2)
(1) ve (2) denklemlerini taraf tarafa toplarsak ve çıkanı 2ye bölersek yeni denklem f i verir.
2f=-2x+4 f=-x+2
(1) ve (2) denklemlerini taraf tarafa çıkarır ve çıkanı 2 ye bölersek yeni denklem g yi verir.
2g=2x²-8x+8 g=x²-4x+4=(x-2)²
Bizden istenilen |f(x)|=g(x) şartını sağlayan x değerleridir. O zaman ;
|2-x|=(x-2)²
=> 2-x = (x-2)² x=2 , x=1
=> x-2 = (x-2)² x=2 , X=3 bu şartı sağlayan 3 tane x değeri vardır . 3,2,1 . 3+2+1=6
x=0 için y=6 olacağından 6a=6 a=1 olur yani f+g = (x-2)(x-3) = x²-5x+6 ...(1)
f-g = a₂(x-1)(x+2)
x=0 için y=-2 olacağından 2a₂=-2 a²=-1 olur yani f-g =-1(x-1)(x-2)=-x²+3x-2 ...(2)
(1) ve (2) denklemlerini taraf tarafa toplarsak ve çıkanı 2ye bölersek yeni denklem f i verir.
2f=-2x+4 f=-x+2
(1) ve (2) denklemlerini taraf tarafa çıkarır ve çıkanı 2 ye bölersek yeni denklem g yi verir.
2g=2x²-8x+8 g=x²-4x+4=(x-2)²
Bizden istenilen |f(x)|=g(x) şartını sağlayan x değerleridir. O zaman ;
|2-x|=(x-2)²
=> 2-x = (x-2)² x=2 , x=1
=> x-2 = (x-2)² x=2 , X=3 bu şartı sağlayan 3 tane x değeri vardır . 3,2,1 . 3+2+1=6
2)
3 ve daha büyük değerler için lnx eğrisinin üst kısmı çizilmiş.3'te 0 değerini aldığı için ln1=0'dan ln(x-2)'nin grafiğinin çizildiğini söyleyebiliriz.
-3 ve 3 dahil olmak üzere arada 0 değerini almış.
-3'ten küçük sayılar için ise -3'te -5 değerini alan fakat verilen grafik için tanımsız olan doğruyu arıyoruz
Soruda verilen değerler B şıkkı için sağlanıyor.
3)
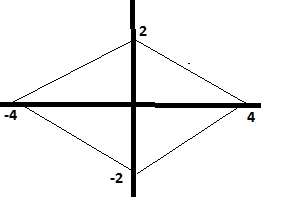
Eğer |x|+|2y|=4 çizilir ve x, 3 birim sağa; y 2 birim yukarı ötelenirse istenen dörtgen elde edilmiş olur.

Biz şimdilik |x|+|2y|=4 dörtgenini kullanalım.
Sayılar tam sayı olacağı için 1. bölgede eksenler dışında (2,1) noktasının sağladığını görürüz.Bu aynı zamanda diğer bölgeler için de sağlandığı için (2,1),(-2,1),(-2,-1),(2,-1) noktalarının da sağlandığını görürüz.Aynı zamanda şuan ötelenmemiş haliyle eksenler üzerinde de dört noktada bulunduğu için dörtgenin üzerinde toplamda 8 nokta vardır.Öteleme yapmamız bunu değiştirmez.
İç bölgesinde ise 1,1 -1,-1 -1,1 1,-1 noktaları iç bölgede sağlar, eksenler üzerinde x ya da y'den biri 0 olduğunda ise 3 tane y ekseni üzerinde, 7 tane x ekseni üzerinde sağlar.Burada 0'ı iki kere saydık bu yüzden 1 tane eksik olarak toplayacağız.
4+3+7-1=13 nokta iç bölgesindedir.
3. öncülde de ilk yazdığımız, dörtgen üzerindeki noktaları öteleyeceğiz.
(2,1),(-2,1),(-2,-1),(2,-1),(0,-2),(0,2),(4,0),(-4,0)
3 br sağa, 2 br yukarı öteliyoruz.
(5,3)
(1,3)
(1,1)
(5,1)
(3,0)
(3,4)
(7,2)
(-1,2) noktalarımız bunlardan 3 tanesi y>x şartını sağlar.
1 ve 2 buldum ben cevabı ama hata olmuş olabilir foruma geçirirken.Siz de kontrol edersiniz, mantık bu.
3 ve daha büyük değerler için lnx eğrisinin üst kısmı çizilmiş.3'te 0 değerini aldığı için ln1=0'dan ln(x-2)'nin grafiğinin çizildiğini söyleyebiliriz.
-3 ve 3 dahil olmak üzere arada 0 değerini almış.
-3'ten küçük sayılar için ise -3'te -5 değerini alan fakat verilen grafik için tanımsız olan doğruyu arıyoruz
Soruda verilen değerler B şıkkı için sağlanıyor.
3)
Eğer |x|+|2y|=4 çizilir ve x, 3 birim sağa; y 2 birim yukarı ötelenirse istenen dörtgen elde edilmiş olur.
Biz şimdilik |x|+|2y|=4 dörtgenini kullanalım.
Sayılar tam sayı olacağı için 1. bölgede eksenler dışında (2,1) noktasının sağladığını görürüz.Bu aynı zamanda diğer bölgeler için de sağlandığı için (2,1),(-2,1),(-2,-1),(2,-1) noktalarının da sağlandığını görürüz.Aynı zamanda şuan ötelenmemiş haliyle eksenler üzerinde de dört noktada bulunduğu için dörtgenin üzerinde toplamda 8 nokta vardır.Öteleme yapmamız bunu değiştirmez.
İç bölgesinde ise 1,1 -1,-1 -1,1 1,-1 noktaları iç bölgede sağlar, eksenler üzerinde x ya da y'den biri 0 olduğunda ise 3 tane y ekseni üzerinde, 7 tane x ekseni üzerinde sağlar.Burada 0'ı iki kere saydık bu yüzden 1 tane eksik olarak toplayacağız.
4+3+7-1=13 nokta iç bölgesindedir.
3. öncülde de ilk yazdığımız, dörtgen üzerindeki noktaları öteleyeceğiz.
(2,1),(-2,1),(-2,-1),(2,-1),(0,-2),(0,2),(4,0),(-4,0)
3 br sağa, 2 br yukarı öteliyoruz.
(5,3)
(1,3)
(1,1)
(5,1)
(3,0)
(3,4)
(7,2)
(-1,2) noktalarımız bunlardan 3 tanesi y>x şartını sağlar.
1 ve 2 buldum ben cevabı ama hata olmuş olabilir foruma geçirirken.Siz de kontrol edersiniz, mantık bu.
f(x)= |50-2x²|-|x²-25|
f(x)=2|x²-25|-|x²-25|
f(x)=|x²-25|
x 5'ten büyük ya da -5'ten küçük ise = x²-25
x 5 ile -5 arasında ise = 25-x²
Eşitliği istediğiniz yere koyabilirsiniz, fonksiyon sürekli.
f(x)=2|x²-25|-|x²-25|
f(x)=|x²-25|
x 5'ten büyük ya da -5'ten küçük ise = x²-25
x 5 ile -5 arasında ise = 25-x²
Eşitliği istediğiniz yere koyabilirsiniz, fonksiyon sürekli.
f(x) çift ise f(x)=f(-x)
f(x)+ x. f(-x) + x². f(-x) = x⁴+x³+2x²+x+1
f(x)+xf(x)+x²f(x)=x⁴+x³+2x²+x+1
f(x)(1+x+x²)=x⁴+x³+2x²+x+1
Bölerseniz
f(x)=x²+1
f(2x)=f(-2x)=4x²+1
f(x)+ x. f(-x) + x². f(-x) = x⁴+x³+2x²+x+1
f(x)+xf(x)+x²f(x)=x⁴+x³+2x²+x+1
f(x)(1+x+x²)=x⁴+x³+2x²+x+1
Bölerseniz
f(x)=x²+1
f(2x)=f(-2x)=4x²+1
