integral soruları

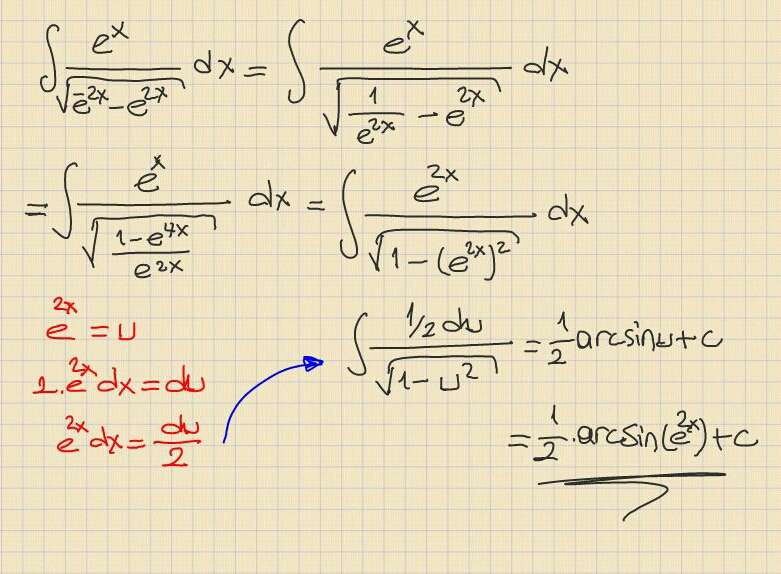
∫ e^x /√e^-2x−e^2x =?

∫tan⁵x.cot⁴x dx =?

∫5^x/√1-25^x dx =?

3∫x².cosx dx -∫x³.sinx dx =?

∫1-cos2x/1+cos2x dx= ?

2.)

∫tan⁵x.cot⁴x dx=∫tanx.tan⁴x.cot⁴x.dx=∫tanxdx

=∫sinx/cosxdx=-ln(cosx)+c

3.)

∫5^x/√1-25^x dx

5^x=u olsun

5^x.ln5dx=du

5^xdx=du/ln5




=1/ln5.arcsinu+c

=1/ln5.arcsin(5^x)+c

4.)

türev....İntegral
..x²..........cosx
.2x..........sinx
.2...........-cosx
.0...........-sinx , ...........(x² den başlayıp çapraz çarpım yapılır +,-,+,... olarak)

∫x².cosx dx=x².sinx+2x.cosx-2.sinx+c

diğerine de sen bakarsın

5.)










=∫tan²xdx

=∫(tan²x+1-1)dx

=tanx-x+c

çok teşekkürler emğine sağlık ) çok iyi anladım yalnız 4. sorunnuun başka bir yolu olabileceğini düşünmüşütüm yoksa bende öyle yapacaktım uzun gibi geldi

4. soru için (x³cosx )' = 3x² cosx -x³ sinx olduğuna dikkat ederseniz aradığınız sonuç x³cosx + C olur.

Yani kısmi integrali bir defa deneyince integraller sadeleşecek ve sonuca daha kısa yoldan gidebilecektiniz.