
C-3) BD ve DC 3 ve 5 ise açıortay oranlarından AB'ye 3k, AC'ye 5k yazabiliriz. Pisagordan k=2 çıkar. O zaman AB=3.k=3.2=6 dır. taralı bölgenin alanı 6.5/2=15 br²
C-4) 12.5/2=30 br² BDC üçgeninin alanıdır. BDC üçgeninde açıortaydan BE 3k ise EC k dır. 4k ya 30 br² düşüyorsa 3k ya yani BDE üçgenine 22,5 br² düşer.
C-4) 12.5/2=30 br² BDC üçgeninin alanıdır. BDC üçgeninde açıortaydan BE 3k ise EC k dır. 4k ya 30 br² düşüyorsa 3k ya yani BDE üçgenine 22,5 br² düşer.
C-2) 
D noktasından bir AC ye bir dik çizersek Bu dik BD ye eşit olacaktır (açıortay üzerinden kenarlara inilen dikler eşit uzunluktadır ve bu dikin indiği noktadan A ya kadar olan uzunluk AB ye eşittir). Ayrıca ADC üçgeni ikizkenar olduğu için bu dik EC yi ikiye böler. k, k dersek EC=AE olduğu için AE de 2k olacaktır. Resimdeki oranlar oluşur. Şimdi açırtaydan 3k ya 3 düşmüşse 4k DC düşer. Yani DC 4 dür.

D noktasından bir AC ye bir dik çizersek Bu dik BD ye eşit olacaktır (açıortay üzerinden kenarlara inilen dikler eşit uzunluktadır ve bu dikin indiği noktadan A ya kadar olan uzunluk AB ye eşittir). Ayrıca ADC üçgeni ikizkenar olduğu için bu dik EC yi ikiye böler. k, k dersek EC=AE olduğu için AE de 2k olacaktır. Resimdeki oranlar oluşur. Şimdi açırtaydan 3k ya 3 düşmüşse 4k DC düşer. Yani DC 4 dür.
C-6) D den AC ye çizilecek yükseklik DH a eşit olacaktır (açıortay üzerinden kenarlara inilen dikler eşit uzunluktadır).
A(ADC)=4.16/2=32
A(DBC)=4.x/2=2x
A(ABC)=32+2x=44
x=6
A(ADC)=4.16/2=32
A(DBC)=4.x/2=2x
A(ABC)=32+2x=44
x=6

sağol Baran. Ayrıca öğrencilerin sorularına yardımcı oluyorsun. Bizim yükümüzü azaltıyorsun. Onun içinde teşekkürler.
Çok teşekkür ediyorum..
Duygu 8. soruda bi eksiklik yok değilmi? bir çözüm göremedim. veri az gibi geldi.
Duygu 8. soruda bi eksiklik yok değilmi? bir çözüm göremedim. veri az gibi geldi.
C-8) önemli değil.

DEC açısı a ise BAC açısı 2a dır.
BAC açısını a,a diye parçalayacak şekilde bir doğru parçası çizelim. HAC açısı ile DEC açısı a olduğu için Bu iki doğru parçası paraleldir. O zaman AHC açısı 90 olur. A açısı a,a diye açıortay ve tabanda aynı zamanda yükseklik varsa bu üçgen ikizkenardır. |AB|=|AC| ve yükselik tabanı 2 eşit parçaya böler. DC=k ise taban 4k dır. taban iki eşit parça olacağından |BH|=2k ve |HD|=k olacaktır. AHC ile EDC üçgenlerindeki benzerrlikten EC=x olacaktır. |AB|=|AC| idi 10=2x =>x=5
diğerleride yarına kalsın geç oldu.
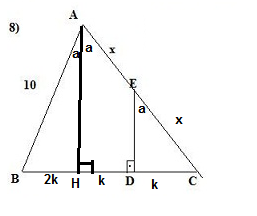
DEC açısı a ise BAC açısı 2a dır.
BAC açısını a,a diye parçalayacak şekilde bir doğru parçası çizelim. HAC açısı ile DEC açısı a olduğu için Bu iki doğru parçası paraleldir. O zaman AHC açısı 90 olur. A açısı a,a diye açıortay ve tabanda aynı zamanda yükseklik varsa bu üçgen ikizkenardır. |AB|=|AC| ve yükselik tabanı 2 eşit parçaya böler. DC=k ise taban 4k dır. taban iki eşit parça olacağından |BH|=2k ve |HD|=k olacaktır. AHC ile EDC üçgenlerindeki benzerrlikten EC=x olacaktır. |AB|=|AC| idi 10=2x =>x=5
diğerleride yarına kalsın geç oldu.
Diğer çözümlü sorular alttadır.
.10. sınıf Açıortay Çözümlü Sorular Açıortay ile İlgili Çözümlü Sorular Çözümlü Açıortay Soruları Çözümlü Geometri Soruları Kenarortay Çözümlü Sorular Kenarortay ile İlgili Sorular Kenarortay Soruları Üçgende Uzunluk Soruları ve Çözümleri
Tüm Etiketler
Tüm Etiketler
