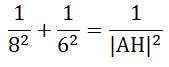geometri-vektörler

1)
"Bunları hepsinin üstünde vektör sembolü var."
A,B,C,D noktaları için DB + AC= CD olduğuna göre aşağıdakilerden hangisi daima doğrudur? (D)

A) AC // BD C) AB=CD
B) AB dik CD D) AB//CD E) AC dik BD


2)

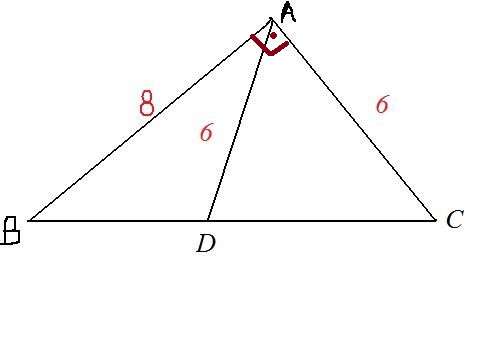
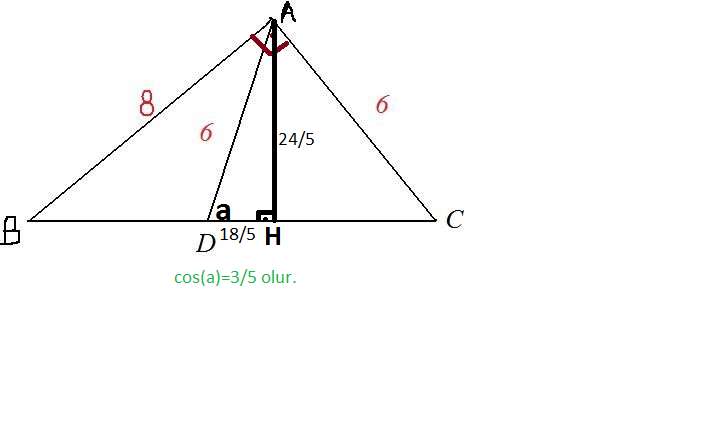
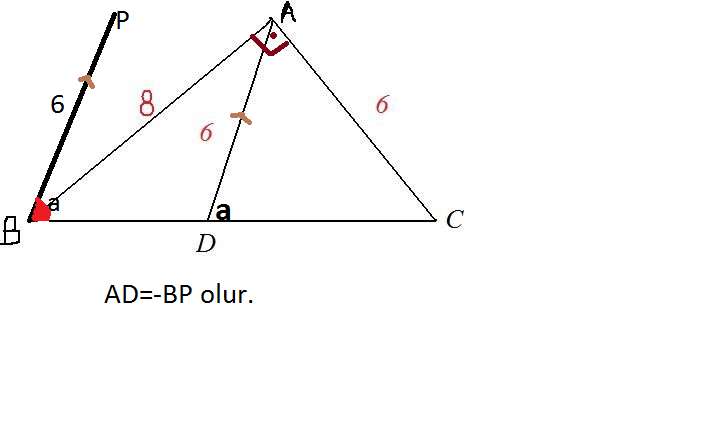
ABC bir üçgen
|AB| =8br

|AD|=|AC| =6br AB vektörü . AC vektörü = 0

Şekilde AD vektörü . BC vektörü çarpımının değeri kaçtır? (-36)

1)
"Bunları hepsinin üstünde vektör sembolü var."
A,B,C,D noktaları için DB + AC= CD olduğuna göre aşağıdakilerden hangisi daima doğrudur? (D)

C.)
DB+AC=CD
B-D+C-A=D-C
B-A= 2D-2C
AB=2.CD
Tanım : a,b ∈ V ve k ∈ R olmak üzere a=k.b ise a ve b vektörleri lineer bağımlıdır. Yani paraleldir. a // b 'dir.
Dolayısıyla AB // CD

Öklid iç çarpımı 0 olan iki vektör birbirine diktir.

A 'dan BC'ye dikme inelim.

|AH|'nu öklitten bulduk:

|DH|'nu da pisagordan veya 3-4-5'in 6/5 katından bulabiliriz. |DH|=18/5 olur.

cos(a)=3/5 oldu.
Zaten ADC=ACD olduğu için cos(a)=3/5 diyebilirdik. Neyse..

Yukarıda da B'den geçen DA'ya paralel olan ve uzunluğu 6 br olan bir doğru parçası çizdik. Otomatik olarak AD=-BP oldu.
Dolayısıyla; <AD,BC>=<-BP,BC>=-<BP,BC>=-1.|BP|.|BC|.cos(a)=-1.6.10.3/5=-36 olur.

Bunu özellikle ayrı bir mesajda veriyorum dikkat çeksin diye: 2. soruda BP'nin çizilmesindeki amaç kosinüslü iç çarpım formülünü kullanabilmekti. Çünkü kosinüslü iç çarpım formülünde kosinüsü alınan açı; vektörlerin başlangıç noktaları arasındaki açıdır. Dolayısıyla iki vektörün öklid iç çarpımını almak için vektörlerden birini (ya da ikisini de) taşıyıp başlangıç noktalarını üst üste getirip oluşan açının kosinüsünü almak, bir yöntemdir.

teşekkür ederim )