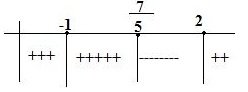Eşitsizliğin çözüm kümesini bulmak için, verilen ifadenin işareti incelenir. İfade sıfıra eşitlenip denklemin kökleri bulunarak tabloda yazılıp çözüm bölgesi bulunur.
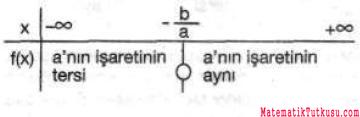
1) Birinci Dereceden Bir Bilinmeyenli Eşitsizlikler:
a ≠ 0 ve a,b ∈ R olmak üzere ax+b > 0, ax+b < 0, ax+b ≥ 0, ax+b ≤ 0, şeklindeki ifadelerdir.
f(x)=ax+b=0 yazılırsa x=-b/a
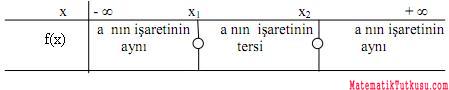
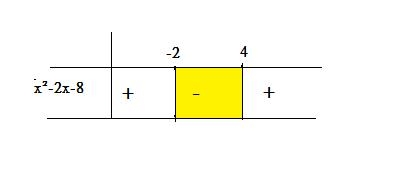
2) İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler:
f(x)=ax2+bx+c olmak üzere:
f(x) < 0, f(x) > 0, f(x) ≤ 0, f(x) ≥ 0 şeklindeki eşitsizliklerdir.
A)<0 ise ax2+bx+c=0 denkleminin gerçel kökleri yoktur.
B)=0 ise ax2+bx+c=0 denkleminde eşit iki kök vardır.
C)>0 ise ax2+bx+c=0 denkleminin x1 ve x2 gibi farklı iki gerçel kökü vardır.