Eşitsizliğin çözüm kümesini bulmak için, verilen ifadenin işareti incelenir. İfade sıfıra eşitlenip denklemin kökleri bulunarak tabloda yazılıp çözüm bölgesi bulunur.
1) Birinci Dereceden Bir Bilinmeyenli Eşitsizlikler:
a ≠ 0 ve a,b ∈ R olmak üzere ax+b > 0, ax+b < 0, ax+b ≥ 0, ax+b ≤ 0, şeklindeki ifadelerdir.
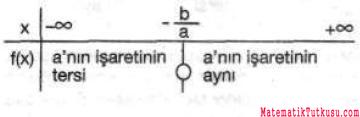
f(x)=ax+b=0 yazılırsa x=-b/a

2) İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler:
f(x)=ax2+bx+c olmak üzere:
f(x) < 0, f(x) > 0, f(x) ≤ 0, f(x) ≥ 0 şeklindeki eşitsizliklerdir.
A) <0 ise ax2+bx+c=0 denkleminin gerçel kökleri yoktur.
<0 ise ax2+bx+c=0 denkleminin gerçel kökleri yoktur.

B) =0 ise ax2+bx+c=0 denkleminde eşit iki kök vardır.
=0 ise ax2+bx+c=0 denkleminde eşit iki kök vardır.

C) >0 ise ax2+bx+c=0 denkleminin x1 ve x2 gibi farklı iki gerçel kökü vardır.
>0 ise ax2+bx+c=0 denkleminin x1 ve x2 gibi farklı iki gerçel kökü vardır.

1) Birinci Dereceden Bir Bilinmeyenli Eşitsizlikler:
a ≠ 0 ve a,b ∈ R olmak üzere ax+b > 0, ax+b < 0, ax+b ≥ 0, ax+b ≤ 0, şeklindeki ifadelerdir.
f(x)=ax+b=0 yazılırsa x=-b/a
2) İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler:
f(x)=ax2+bx+c olmak üzere:
f(x) < 0, f(x) > 0, f(x) ≤ 0, f(x) ≥ 0 şeklindeki eşitsizliklerdir.
A)
 <0 ise ax2+bx+c=0 denkleminin gerçel kökleri yoktur.
<0 ise ax2+bx+c=0 denkleminin gerçel kökleri yoktur.
B)
 =0 ise ax2+bx+c=0 denkleminde eşit iki kök vardır.
=0 ise ax2+bx+c=0 denkleminde eşit iki kök vardır.
C)
 >0 ise ax2+bx+c=0 denkleminin x1 ve x2 gibi farklı iki gerçel kökü vardır.
>0 ise ax2+bx+c=0 denkleminin x1 ve x2 gibi farklı iki gerçel kökü vardır.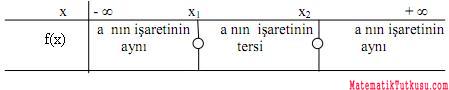
3) f(x)=M(x).N(x).R(x) çarpım şeklinde biçimindeki ifadelerin işareti incelenirken çarpanların herbiri ayrı ayrı sıfıra eşitlenip kökler bulunur. Bulunan kökler tabloya yazılır. Çarpanların herbirinden en büyük üslü terimler alınıp çarpılır.
Sonra elde edilecek axn şeklindeki ifade de a'nın işareti +∞ tarafa(en sağa) yazılarak, her kökte işaret değiştirilerek tablo işaretlenir. Ancak çift kat köke rastlandığında işaret değiştirilmez.
T(x)/Q(x) şeklindeki ifadeler T(x).Q(x) şeklideymiş gibi düşünülerek işlem yapılır. Fakat paydayı sıfır yapan x değerleri ifadeyi tanımsız yapacağından; çözüm aralığına dahil edilmezler.
Sonra elde edilecek axn şeklindeki ifade de a'nın işareti +∞ tarafa(en sağa) yazılarak, her kökte işaret değiştirilerek tablo işaretlenir. Ancak çift kat köke rastlandığında işaret değiştirilmez.
T(x)/Q(x) şeklindeki ifadeler T(x).Q(x) şeklideymiş gibi düşünülerek işlem yapılır. Fakat paydayı sıfır yapan x değerleri ifadeyi tanımsız yapacağından; çözüm aralığına dahil edilmezler.
İkinci Dereceden Bir Bilinmeyenli Eşitsizliklerin Köklerin İşaretleri
ax2+bx+ c denkleminin kökleri x1 ve x2 olsun.
1) x1.x2<0 ise, ters işaretli iki gerçel kök vardır. Bu durumda;
a) x1+x2>0 ise mutlak değeri büyük olan kök pozitiftir.
b) x1+x2<0 ise mutlak değeri büyük olan kök negatiftir.
c) x1+x2=0 ise köklerin mutlak değerleri eşittir.
2) x1.x2 >0 ve
 ≥ 0 ise, denklemin aynı işaretli iki gerçel kökü vardır. Bu durumda;
≥ 0 ise, denklemin aynı işaretli iki gerçel kökü vardır. Bu durumda;a) x1+x2>0 ise iki kök de pozitiftir.
b) x1+x2<0 ise iki kök de negatiftir.
3) 1.x2=0 ise, denklemin köklerinden en az biri sıfırdır. Bu durumda;
a) x1+x2>0 ise x1=0, x2>0
b) x1+x2<0 ise x1=0, x2<0
c) x1+x2=0 ise x1=x2=0 olur.
4)
 ≤ 0 ise, denkleminin gerçel kökleri olmadığından, köklerin işareti söz konusu değildir.
≤ 0 ise, denkleminin gerçel kökleri olmadığından, köklerin işareti söz konusu değildir. 1. Dereceden Eşitsizlikler:
ÖRNEK 1:
eşitsizliğini sağlayan x'in en küçük tam sayı değeri kaçtır ?
ÇÖZÜM 1:
5-8x<13.3
5-8x<39
-8x<34 ("-" ile çarparsak eşitsizlik yön değiştirir)
8x>-34
Buna göre x>-4.25 olduğundan x'in en küçük tam sayı değeri -4 bulunur.
ÖRNEK 1:
5-8x
13
<3
eşitsizliğini sağlayan x'in en küçük tam sayı değeri kaçtır ?
ÇÖZÜM 1:
5-8x
13
<3
5-8x<13.3
5-8x<39
-8x<34 ("-" ile çarparsak eşitsizlik yön değiştirir)
8x>-34
x>-
34
8
x>-
17
4
Buna göre x>-4.25 olduğundan x'in en küçük tam sayı değeri -4 bulunur.
1. dereceden eşitsizlikler:
ÖRNEK 2:
-10<5-3x≤19
koşulunu sağlayan x tamsayı değerleri toplamı kaçtır ?
-10<5-3x≤19
-15<-3x≤14
Bu aralıkta x'in tam sayı olduğu değerlerin toplamı
(-4)+(-3)+(-2)+(-1)+0+1+2+3+4=0 bulunur.
ÖRNEK 2:
-10<5-3x≤19
koşulunu sağlayan x tamsayı değerleri toplamı kaçtır ?
-10<5-3x≤19
-15<-3x≤14
-5<-x≤-
14
3
5>x≥-
14
3
Bu aralıkta x'in tam sayı olduğu değerlerin toplamı
(-4)+(-3)+(-2)+(-1)+0+1+2+3+4=0 bulunur.
2. dereceden eşitsizlikler:
ÖRNEK 3:
x²-2x-8≤0
eşitsizliğinin çözüm kümesi nedir ?
Delta>0 olduğundan
x²-2x-8=(x-4).(x+2)=0
x₁=4, x₂=-2
Buna göre tablo oluşturalım eşitsizliğin işareti (+) olduğundan tablo (+) ile başlar.

Eşitlik olduğundan kapalı aralıktır.
Buna göre Ç.K=[-2,4] veya Ç.K= -2≤x≤4
ÖRNEK 3:
x²-2x-8≤0
eşitsizliğinin çözüm kümesi nedir ?
Delta>0 olduğundan
x²-2x-8=(x-4).(x+2)=0
x₁=4, x₂=-2
Buna göre tablo oluşturalım eşitsizliğin işareti (+) olduğundan tablo (+) ile başlar.
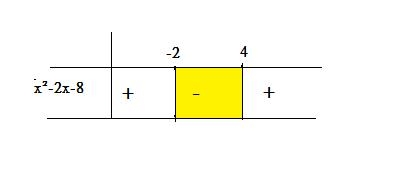
Eşitlik olduğundan kapalı aralıktır.
Buna göre Ç.K=[-2,4] veya Ç.K= -2≤x≤4
2. dereceden eşitsizlikler:
ÖRNEK 4:
ÇÖZÜM 3:
5x-7=0 =>x=7/5
x-2=0 =>x=2 (paydayı sıfır yapar)
x+1=0=>x=-1(paydayı sıfır yapar)

Tabloya bakarsak işareti negatif olan bölgeleri arıyoruz Bu durumda ;
ÖRNEK 4:
x-1
x-2
≤
x-3
x+1
Eşitsizliğinin çözüm kümesini bulunuz.
ÇÖZÜM 3:
x-1
x-2
-
x-3
x+1
≤0
(x-1).(x+1)-(x-3).(x-2)
(x-2).(x+1)
≤0
(x²-1)-(x²-5x+6)
(x-2).(x+1)
≤0
5x-7
(x-2).(x+1)
≤0
5x-7=0 =>x=7/5
x-2=0 =>x=2 (paydayı sıfır yapar)
x+1=0=>x=-1(paydayı sıfır yapar)
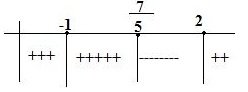
Tabloya bakarsak işareti negatif olan bölgeleri arıyoruz Bu durumda ;
Ç.K=(-&,-1)∪[
7
5
,2)
