Sayın hocalarım, Limitte delta epsilon tekniğini tam olarak anlayamadım,açıkçası mantık olarak sadece şunu anladığımı söyleyebilirim. Delta -> x ekseninde çok ufak değerleri ifade ediyor. Aynı şekilde epsilonda y ekseninde, bizim her x değişimimiz yani ufacık delta değişimimiz y ekseninde de ufacık bir epsilon değişikliğine sebep oluyor. Benim anladığım bu ve bu kadar. yanlışım varsa yardımcı olursanız sevinirim. Asıl sorunum ise bunu soruya gelince nasıl çözeceğimi ne yapacağımı bilemiyorum. Bana resimdeki sorular üzerinde adım adım anlatabilirseniz çok sevinirim. Teşekkürler

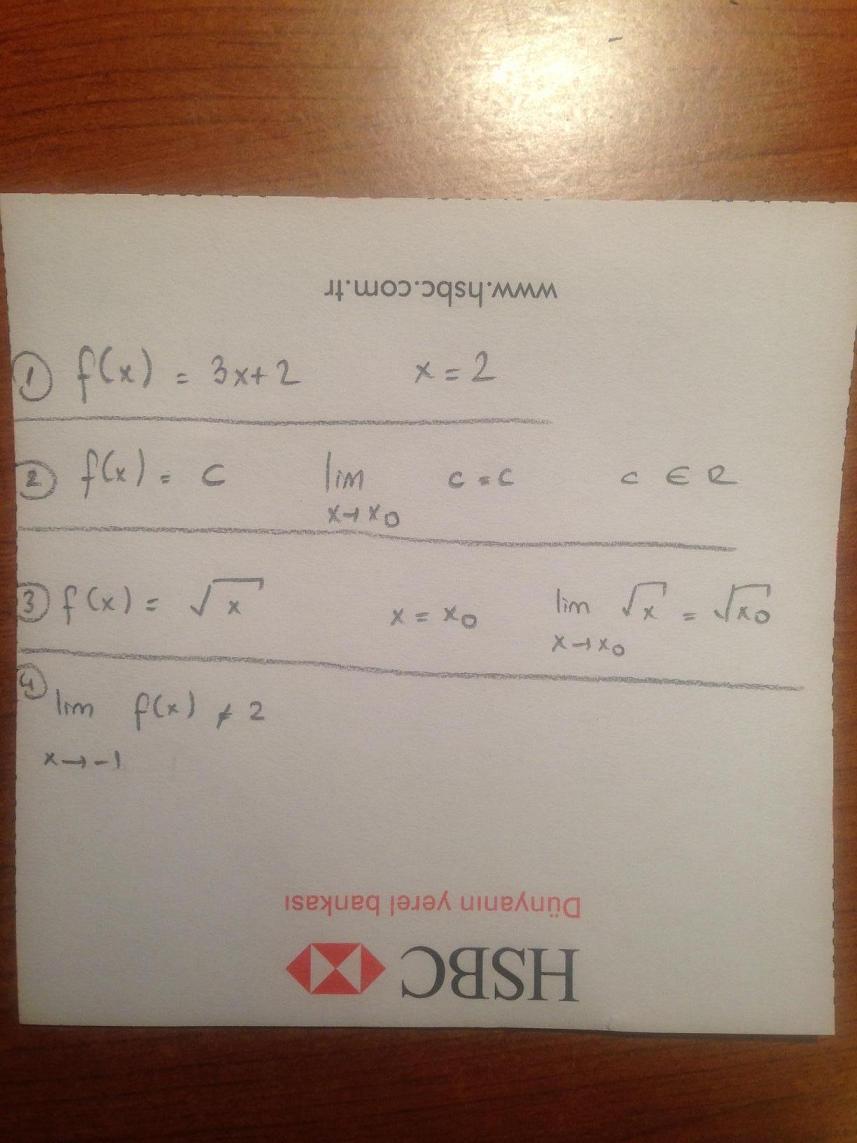
Limitin tanımı değil mi bu ? Konuyu çalıştığınız kitap varsa veya defterde tanım varsa ben tanımı açıklayabilirim..
Ayrıca yazılabilecek soruların resimle sorulması yasak,sorular çok karmaşık değil editörle basitçe yazılabiliyor..
Ayrıca yazılabilecek soruların resimle sorulması yasak,sorular çok karmaşık değil editörle basitçe yazılabiliyor..
Özür dilerim yasak olduğu hakkında bilgim yoktu. Elimde şuanda bununla ilgili bir not yok malesef,epsilon yöntemini anlamış değilim ve bunları nasıl çözeceğim hakkında bir fikrim yok
Tamam tanımları bir üniversite dökümanında buldum..Tanımı açıklamaya çalışayım,tanıma göre de ilk sorunuzu çözeyim,diğerlerini kendiniz hâlletmeye çalışırsınız..
Yığılma noktası bilinmeden limit kavramı anlaşılamaz..Önce yığılma noktasının da tanımını verelim..
A kümesi IR sayılar kümesinin bir alt kümesi ve y∈IR olsun..Eğer ε>0 sayısı için
|a-y|<ε olacak şekilde A'nın y'den farklı bir a elemanı bulunabiliyorsa y noktasına A kümesinin bir yığılma noktası denir..Ayrıca tanımdan yığılma noktasının A kümesine ait olabileceği veya olmayabileceğini de anlıyoruz..
Şimdi yukarıdaki tanım bize diyor ki..Öncelikle reel sayılar kümesinden bir A kümesi tanımlıyoruz,ardından reel sayılar kümesinde bir y elemanı seçiyoruz..ε burada uzaklığı temsil ediyor,çünkü mutlak değer kullanılmış..
Her ε uzaklığı için |a-y|<ε olacak şekilde A kümesinde y'den farklı bir a elemanı bulunabiliyorsa(a burada keyfi bir eleman) y noktası yığılma noktası..Bu da demek oluyor ki y'ye olan uzaklığı ε değerinden küçük olmak şartıyla y'den farklı bir a elemanı bulabiliyorsak y yığılma noktasıdır..Örnek vereyim..
Reel sayılar kümesinde [1,3] aralığını ele alalım..Bu aralıktan y=2 değerini alalım.ε=1 olsun..Tanıma göre |a-2|<ε olacak şekilde 2'den farklı bir eleman bulabiliyorsak 2 noktası bir yığılma noktasıdır..a'nın y=2'ye olan uzaklığnın ε=1'den küçük olmak şartına uygun olması için a'yı (1,3) aralığında herhangi bir nokta seçebiliriz..Örneğin a=1,3 noktası olsun..|1,3-2|<ε=1 oluyor mu ? |-0,7|<ε=1 ve nihayet 0,7<ε=1 oldu..Demek ki 2 noktası bu kümenin yığılma noktasıymış..Ama uzaklığın her ε için olması gerektiğini söylüyor tanım..Peki biz ε uzaklığını 1 değil de,1/2 veya 1/3 alsaydık gene de 2 yığılma noktası olmaz mıydı ? Sayı doğrusu çizerek de görülebilir ki,ε uzaklığı ne olursa olsun y'den farklı bir a sayısı bulunabilir..Çünkü biz A kümesini reel sayılar içinden aldık ve her reel sayının arasında muhakkak bir (hatta ne biri sonsuz tane) reel sayı vardır
Peki A'yı doğal sayılar kümesinden seçseydik ?
[1,3] aralığını alalım..Burada kümemiz {1,2,3} elemanlarından oluşacaktır..
y=2'nin bu durumda da yığılma noktası olup olmadığını kontrol edelim..
ε=0,5 alalım..y=2 noktasından 0,5 uzaklığını alalım sağdan ve soldan..(Mutlak değer demek sağdan ve soldan almak demek,mesele mutlak değerse uzaklık vardır)
1,5 ve 2,5 aralığında y=2'den başka bir a elemanı bulabiliyor muyuz ? Kümemiz sadece 1,2,3 elemanlarından oluştuğu için burada ((1,5),(2,5)) aralığında 2'den (yâni y'den) farklı bir eleman bulamadık..Demek ki bu şekilde bir küme için 2 noktası yığılma noktası değilmiş..
Limitin tanımına geçelim..
A⊂R olmak üzere f A'dan R'ye bir fonksiyon ve a da A kümesinde bir yığılma noktası olsun..
Her ε>0 için eğer 0<|x-a|<δ olduğunda |f(x)-L|<ε kalacak şekilde bir δ>0 sayısı bulunabiliyorsa x, a'ye yaklaştığında fonksiyonun limiti L denir..
f(x)=L biçiminde gösterilir..
Dikkat edersek A'yı IR kümesinden alıyorlar,neden ? Çünkü her ε>0 için (ε uzaklığı için) arada sayılar bulmalıyız..Tanıma göre x'den δ kadar sağdan ve soldan bir uzaklık aldığımızda bu aralık ((x-δ),(x+δ)) oluyor..Bu aralığın içinde bir a sayısı aldığımızda (bakın tanımda x-a'nın mutlak değeri δ'dan küçükmüş,demek ki a bu aralığın içinde olmalı) Aynı zamanda x'in fonksiyondaki görüntüsü olan f(x)'in de ε kadar üstten ve alttan (çünkü görüntü y ekseninde) uzaklık aldığımızda bu aralık ((f(x)-ε),(f(x)+ε)) oluyor..Bu y eksenindeki aralıktan da bir L noktası seçtiğimizde (tanıma göre f(x)-L'nin mutlak değeri ε'den küçük olmak zorunda) hiçbir sorun olmadan tüm durumlar sağlanıyorsa,bu L noktası x a'ya yaklaştığında fonksiyonun limiti oluyor..
Kısa x'ten çook minik bir uzaklık aldığımızda ve bu uzaklığın arasında bir a noktası seçtiğimizde,bu a noktasının grafikte gösterdiği (o noktada tanımlı olmasa bile,tanımlı olsaydı gideceğini hissettiğimiz) bir L noktası da,x'in görüntüsü olan f(x)'ten çook minik bir uzaklığın arasında kalıyorsa bu L noktası limittir..
Bir tanım daha :
Fonksiyonun limiti L ise ε>0 verildiğinde öyle bir δ>0 bulunabilir ki,x≠a için y=f(x) grafiğinin x=a-δ ve x=a+δ düşey doğruları arasında kalan noktaları y=L-ε ve y=L+ε yatay doğruları arasında bulunur..
Bunu limiti bize verildiğinde ama limitin doğru olduğu kanıtlanmak istenildiğinde kullanıyormuşuz..
f(x)=3x+2 x=2'deki limitinin 8 olduğunu göstermemiz istenmiş sanırım..
ε>0 alalım..Limiti 8 ise y=8-ε ve y=8+ε doğrularının 3x+2 doğrusunu kestiği noktaların apsislerini bulalım..Çünkü şu son tanıma göre y=L-ε ve y=L+ε yatay doğruları arasında kalan noktaların x=a-δ ve x=a+δ doğrularının arasında kalması lâzım..
3x+2=8-ε buradan x=(6-ε)/3 ve x=2-(ε/3)
3x+2=8+ε buradan x=(6+ε)/3 ve x=2+(ε/3) bulunur..
Bu bize ne anlatıyor..x=2 noktasından (ε/3) kadar sağdan ve soldan uzaklık aldığımızda bu aralıkta kalan noktaların görüntüleri L=8 olmak üzere 8-ε ve 8+ε noktalarının arasında kalıyormuş..Böylece biz
δ=(ε/3) olacak şekilde bir δ>0 bulabildik..Demek ki x 2'ye yaklaşırken 3x+2'nin limiti 8'miş..Çünkü tanımda bizden istenen tüm durumları sağladı.
Çok uzun bir yazı oldu ve kâğıt kalemsiz yazdığım-çözdüğüm için hatalar yapmış olabilirim,ama doğru açıkladığımı düşünüyorum..Kafanıza takılan bir şey olursa söyleyin..
Yığılma noktası bilinmeden limit kavramı anlaşılamaz..Önce yığılma noktasının da tanımını verelim..
A kümesi IR sayılar kümesinin bir alt kümesi ve y∈IR olsun..Eğer ε>0 sayısı için
|a-y|<ε olacak şekilde A'nın y'den farklı bir a elemanı bulunabiliyorsa y noktasına A kümesinin bir yığılma noktası denir..Ayrıca tanımdan yığılma noktasının A kümesine ait olabileceği veya olmayabileceğini de anlıyoruz..
Şimdi yukarıdaki tanım bize diyor ki..Öncelikle reel sayılar kümesinden bir A kümesi tanımlıyoruz,ardından reel sayılar kümesinde bir y elemanı seçiyoruz..ε burada uzaklığı temsil ediyor,çünkü mutlak değer kullanılmış..
Her ε uzaklığı için |a-y|<ε olacak şekilde A kümesinde y'den farklı bir a elemanı bulunabiliyorsa(a burada keyfi bir eleman) y noktası yığılma noktası..Bu da demek oluyor ki y'ye olan uzaklığı ε değerinden küçük olmak şartıyla y'den farklı bir a elemanı bulabiliyorsak y yığılma noktasıdır..Örnek vereyim..
Reel sayılar kümesinde [1,3] aralığını ele alalım..Bu aralıktan y=2 değerini alalım.ε=1 olsun..Tanıma göre |a-2|<ε olacak şekilde 2'den farklı bir eleman bulabiliyorsak 2 noktası bir yığılma noktasıdır..a'nın y=2'ye olan uzaklığnın ε=1'den küçük olmak şartına uygun olması için a'yı (1,3) aralığında herhangi bir nokta seçebiliriz..Örneğin a=1,3 noktası olsun..|1,3-2|<ε=1 oluyor mu ? |-0,7|<ε=1 ve nihayet 0,7<ε=1 oldu..Demek ki 2 noktası bu kümenin yığılma noktasıymış..Ama uzaklığın her ε için olması gerektiğini söylüyor tanım..Peki biz ε uzaklığını 1 değil de,1/2 veya 1/3 alsaydık gene de 2 yığılma noktası olmaz mıydı ? Sayı doğrusu çizerek de görülebilir ki,ε uzaklığı ne olursa olsun y'den farklı bir a sayısı bulunabilir..Çünkü biz A kümesini reel sayılar içinden aldık ve her reel sayının arasında muhakkak bir (hatta ne biri sonsuz tane) reel sayı vardır
Peki A'yı doğal sayılar kümesinden seçseydik ?
[1,3] aralığını alalım..Burada kümemiz {1,2,3} elemanlarından oluşacaktır..
y=2'nin bu durumda da yığılma noktası olup olmadığını kontrol edelim..
ε=0,5 alalım..y=2 noktasından 0,5 uzaklığını alalım sağdan ve soldan..(Mutlak değer demek sağdan ve soldan almak demek,mesele mutlak değerse uzaklık vardır)
1,5 ve 2,5 aralığında y=2'den başka bir a elemanı bulabiliyor muyuz ? Kümemiz sadece 1,2,3 elemanlarından oluştuğu için burada ((1,5),(2,5)) aralığında 2'den (yâni y'den) farklı bir eleman bulamadık..Demek ki bu şekilde bir küme için 2 noktası yığılma noktası değilmiş..
Limitin tanımına geçelim..
A⊂R olmak üzere f A'dan R'ye bir fonksiyon ve a da A kümesinde bir yığılma noktası olsun..
Her ε>0 için eğer 0<|x-a|<δ olduğunda |f(x)-L|<ε kalacak şekilde bir δ>0 sayısı bulunabiliyorsa x, a'ye yaklaştığında fonksiyonun limiti L denir..
lim
x→a
Dikkat edersek A'yı IR kümesinden alıyorlar,neden ? Çünkü her ε>0 için (ε uzaklığı için) arada sayılar bulmalıyız..Tanıma göre x'den δ kadar sağdan ve soldan bir uzaklık aldığımızda bu aralık ((x-δ),(x+δ)) oluyor..Bu aralığın içinde bir a sayısı aldığımızda (bakın tanımda x-a'nın mutlak değeri δ'dan küçükmüş,demek ki a bu aralığın içinde olmalı) Aynı zamanda x'in fonksiyondaki görüntüsü olan f(x)'in de ε kadar üstten ve alttan (çünkü görüntü y ekseninde) uzaklık aldığımızda bu aralık ((f(x)-ε),(f(x)+ε)) oluyor..Bu y eksenindeki aralıktan da bir L noktası seçtiğimizde (tanıma göre f(x)-L'nin mutlak değeri ε'den küçük olmak zorunda) hiçbir sorun olmadan tüm durumlar sağlanıyorsa,bu L noktası x a'ya yaklaştığında fonksiyonun limiti oluyor..
Kısa x'ten çook minik bir uzaklık aldığımızda ve bu uzaklığın arasında bir a noktası seçtiğimizde,bu a noktasının grafikte gösterdiği (o noktada tanımlı olmasa bile,tanımlı olsaydı gideceğini hissettiğimiz) bir L noktası da,x'in görüntüsü olan f(x)'ten çook minik bir uzaklığın arasında kalıyorsa bu L noktası limittir..
Bir tanım daha :
Fonksiyonun limiti L ise ε>0 verildiğinde öyle bir δ>0 bulunabilir ki,x≠a için y=f(x) grafiğinin x=a-δ ve x=a+δ düşey doğruları arasında kalan noktaları y=L-ε ve y=L+ε yatay doğruları arasında bulunur..
Bunu limiti bize verildiğinde ama limitin doğru olduğu kanıtlanmak istenildiğinde kullanıyormuşuz..
f(x)=3x+2 x=2'deki limitinin 8 olduğunu göstermemiz istenmiş sanırım..
ε>0 alalım..Limiti 8 ise y=8-ε ve y=8+ε doğrularının 3x+2 doğrusunu kestiği noktaların apsislerini bulalım..Çünkü şu son tanıma göre y=L-ε ve y=L+ε yatay doğruları arasında kalan noktaların x=a-δ ve x=a+δ doğrularının arasında kalması lâzım..
3x+2=8-ε buradan x=(6-ε)/3 ve x=2-(ε/3)
3x+2=8+ε buradan x=(6+ε)/3 ve x=2+(ε/3) bulunur..
Bu bize ne anlatıyor..x=2 noktasından (ε/3) kadar sağdan ve soldan uzaklık aldığımızda bu aralıkta kalan noktaların görüntüleri L=8 olmak üzere 8-ε ve 8+ε noktalarının arasında kalıyormuş..Böylece biz
δ=(ε/3) olacak şekilde bir δ>0 bulabildik..Demek ki x 2'ye yaklaşırken 3x+2'nin limiti 8'miş..Çünkü tanımda bizden istenen tüm durumları sağladı.
Çok uzun bir yazı oldu ve kâğıt kalemsiz yazdığım-çözdüğüm için hatalar yapmış olabilirim,ama doğru açıkladığımı düşünüyorum..Kafanıza takılan bir şey olursa söyleyin..
Çok teşekkür ederim elinize sağlık
